হারমোনিক গড়

হারমোনিক মানে কি?

প্রদত্ত পরিসংখ্যানগুলির সুরেলা গড় গণনা করার জন্য, আপনাকে প্রতিটি সংখ্যার পারস্পরিক দ্বারা পর্যবেক্ষণের মোট সংখ্যাকে ভাগ করতে হবে। আসুন একটি উদাহরণ সহ সুরেলা গড় সংজ্ঞা বুঝি।

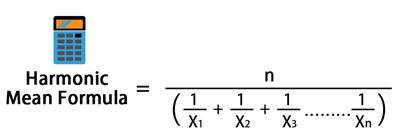
ধরুন আপনাকে 1, 3, 5 এবং 10 এর হারমোনিক গড় গণনা করতে বলা হয়েছে। এখন আপনার মোট 4 টি পর্যবেক্ষণ আছে, আপনি প্রতিটি সংখ্যার পারস্পরিক যোগফল দ্বারা 4 কে ভাগ করবেন, অর্থাৎ 1/1 + 1/3 + 1/5 + 1/10। এই পারস্পরিক যোগফল থেকে প্রাপ্ত মোটকে 4 দ্বারা ভাগ করলে, আপনি এই গণনার হারমোনিক গড় পাবেন।

হারমোনিক গড় একটি ওভারভিউ

সাবকন্ট্রারি গড় হিসাবেও পরিচিত, হারমোনিক গড়কে প্রদত্ত পরিসংখ্যানগুলির গড় গণনা করার জন্য একটি সাধারণ গণনার বিকল্প হিসাবে বিবেচনা করা হয়। এটা মনে রাখা গুরুত্বপূর্ণ যে সুরেলা গড় অবতল হতে হবে। এটি বলার সাথে সাথে, আপনি গড় গণনা করার জন্য যে সংখ্যাগুলি ব্যবহার করেন সেগুলিতে আপনাকে বিশেষ মনোযোগ দিতে হবে। এখানে, আপনি নেতিবাচক সংখ্যা ব্যবহার করতে পারবেন না।

হারমোনিক গড় হল পিথাগোরিয়ান গড়ের একটি অংশ, যা মোট তিনটি উপায় নিয়ে গঠিত (প্রথম এবং দ্বিতীয়টি যথাক্রমে পাটিগণিত গড় এবং জ্যামিতিক গড়)। প্রদত্ত মান একই হলে হারমোনিক গড় পাটিগণিত এবং জ্যামিতিক গড় হিসাবে একই হবে।

উদাহরণস্বরূপ, প্রদত্ত মান 4, 4, এবং 4 হলে তিনটি পিথাগোরিয়ান মানেই 4 হবে। যেহেতু গাণিতিক গড় বেশ সাধারণভাবে ব্যবহৃত হয়, তাই হারমোনিক গড় প্রায়শই পাটিগণিত গড়ের সাথে বিভ্রান্ত হয়। অনেক জায়গায়, হারমোনিক মানে সেরা সম্ভাব্য গড় দেয়। উল্লেখ্য যে হারমোনিক গড় প্রধানত গড় গণনার জন্য ব্যবহৃত হয় যখন প্রদত্ত মান অনুপাত এবং হারে প্রকাশ করা হয়।

পাটিগণিত এবং সুরেলা উপায়গুলি কোথায় গণনা করা হয় তা বোঝার জন্য আমরা আরেকটি উদাহরণ নিতে যাচ্ছি।

হারমোনিক গড় বনাম পাটিগণিত গড়

উদাহরণস্বরূপ, যানবাহনের গতি এবং এর দূরত্ব নিন। ধরা যাক একটি ট্রেন একটি নির্দিষ্ট গতিতে ভ্রমণ করে একটি নির্দিষ্ট দূরত্ব অতিক্রম করেছে। এখন, যদি ফেরার সময় একই দূরত্ব অতিক্রম করে, তাহলে হারমোনিক গড় ব্যবহার করে ট্রেনের গড় গতি গণনা করা হবে। এই গাণিতিক সূত্রটি আপনাকে গড় গতি খুঁজে পেতে সাহায্য করবে যে ট্রেনটি অবশ্যই গন্তব্যে ফিরে এসেছে। যদি এই ট্রেনটি বিভিন্ন গতিতে ভ্রমণ করে তবুও গন্তব্যে পৌঁছাতে সমান সময় নেয়, তাহলে ট্রেনের গড় গতি পেতে আপনাকে পাটিগণিত গড় গণনা করতে হবে।

একই উদাহরণ প্রতিটি গণনার ক্ষেত্রে প্রযোজ্য, যেখানে ব্যবহারকারী দূরত্বের পরিপ্রেক্ষিতে গাড়ির গড় গতি বের করার চেষ্টা করে। যদি আপনার গাড়িটি বিভিন্ন গতিতে একই দূরত্ব কভার করে, তাহলে আপনাকে গাড়ির গড় গতি গণনা করতে হারমোনিক গড় ব্যবহার করতে হবে।