હાર્મોનિક મીન

હાર્મોનિક મીન શું છે?

આપેલ આંકડાઓના હાર્મોનિક સરેરાશની ગણતરી કરવા માટે, તમારે દરેક સંખ્યાના પરસ્પર દ્વારા અવલોકનોની કુલ સંખ્યાને વિભાજીત કરવી જોઈએ. ચાલો એક ઉદાહરણ સાથે હાર્મોનિક સરેરાશ વ્યાખ્યા સમજીએ.

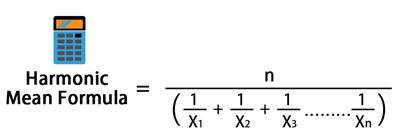
ધારો કે તમને 1, 3, 5 અને 10 ના હાર્મોનિક સરેરાશની ગણતરી કરવાનું કહેવામાં આવે છે. હવે જ્યારે તમારી પાસે કુલ 4 અવલોકનો છે, તો તમે 4 ને દરેક સંખ્યાના પરસ્પર, એટલે કે 1/1 + 1/3ના સરવાળાથી ભાગતા હશો. + 1/5 + 1/10. આ પરસ્પરનાં સરવાળામાંથી તમને મળેલ કુલને 4 વડે ભાગવા પર, તમને આ ગણતરીનો હાર્મોનિક સરેરાશ મળશે.

હાર્મોનિક મીનની ઝાંખી

સબકોન્ટ્રારી મીન તરીકે પણ ઓળખાય છે, આપેલ આંકડાઓની સરેરાશની ગણતરી કરવા માટે હાર્મોનિક સરેરાશને સામાન્ય ગણતરી વિકલ્પ તરીકે ગણવામાં આવે છે. એ નોંધવું અગત્યનું છે કે હાર્મોનિક સરેરાશ અંતર્મુખ હોય છે. તે કહેવાની સાથે, તમારે સરેરાશની ગણતરી કરવા માટે તમે જે સંખ્યાઓનો ઉપયોગ કરો છો તેના પર તમારે વિશેષ ધ્યાન આપવાની જરૂર છે. અહીં, તમે નકારાત્મક સંખ્યાઓનો ઉપયોગ કરી શકતા નથી.

હાર્મોનિક સરેરાશ એ પાયથાગોરિયન સરેરાશનો એક ભાગ છે, જેમાં કુલ ત્રણ માધ્યમનો સમાવેશ થાય છે (પ્રથમ અને બીજો અનુક્રમે અંકગણિત સરેરાશ અને ભૌમિતિક સરેરાશ છે). જો આપેલ મૂલ્યો સમાન હોય તો હાર્મોનિક સરેરાશ અંકગણિત અને ભૌમિતિક સરેરાશ સમાન હશે.

ઉદાહરણ તરીકે, જો આપેલ મૂલ્યો 4, 4 અને 4 હોય તો ત્રણેય પાયથાગોરિયન અર્થ 4 હશે. અંકગણિત સરેરાશનો સામાન્ય રીતે ઉપયોગ થતો હોવાથી, હાર્મોનિક સરેરાશ ઘણીવાર અંકગણિત સરેરાશ સાથે મૂંઝવણમાં હોય છે. ઘણી જગ્યાએ, હાર્મોનિક અર્થ શ્રેષ્ઠ શક્ય સરેરાશ આપે છે. નોંધ કરો કે હાર્મોનિક સરેરાશનો ઉપયોગ મુખ્યત્વે સરેરાશની ગણતરી માટે થાય છે જ્યારે આપેલ મૂલ્ય ગુણોત્તર અને દરોમાં દર્શાવવામાં આવે છે.

અંકગણિત અને હાર્મોનિક માધ્યમની ગણતરી ક્યાં કરવામાં આવે છે તે સમજવા માટે આપણે બીજું ઉદાહરણ લેવા જઈ રહ્યા છીએ.

હાર્મોનિક મીન વિ અંકગણિત મીન

ઉદાહરણ તરીકે, વાહનની ઝડપ અને તેનું અંતર લો. ચાલો કહીએ કે ટ્રેને ચોક્કસ ઝડપે મુસાફરી કરીને ચોક્કસ અંતર કાપ્યું છે. હવે, જો તે પરત ફરતી વખતે સમાન અંતર કાપે છે, તો હાર્મોનિક સરેરાશનો ઉપયોગ કરીને ટ્રેનની સરેરાશ ઝડપની ગણતરી કરવામાં આવશે. આ ગાણિતિક સૂત્ર તમને એવરેજ સ્પીડ શોધવામાં મદદ કરશે કે જેનાથી ટ્રેન ગંતવ્ય પર પાછી આવી હશે. જો આ ટ્રેન જુદી જુદી ઝડપે મુસાફરી કરે છે છતાં ગંતવ્ય સ્થાને પહોંચવામાં સમાન સમય લે છે, તો તમારે ટ્રેનની સરેરાશ ઝડપ મેળવવા માટે અંકગણિત સરેરાશની ગણતરી કરવાની જરૂર પડશે.

આ જ ઉદાહરણ દરેક ગણતરીને લાગુ પડે છે, જેમાં વપરાશકર્તા મુસાફરી કરેલ અંતરને જોતાં વાહનની સરેરાશ ઝડપ શોધવાનો પ્રયાસ કરે છે. જો તમારું વાહન અલગ-અલગ ઝડપે સમાન અંતર કાપે છે, તો તમારે વાહનની સરેરાશ ઝડપની ગણતરી કરવા માટે હાર્મોનિક માધ્યમનો ઉપયોગ કરવાની જરૂર છે.