ಹಾರ್ಮೋನಿಕ್ ಮೀನ್

ಹಾರ್ಮೋನಿಕ್ ಮೀನ್ ಎಂದರೇನು?

ನೀಡಿರುವ ಅಂಕಿಗಳ ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು, ನೀವು ಪ್ರತಿ ಸಂಖ್ಯೆಯ ಪರಸ್ಪರ ಅವಲೋಕನಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯನ್ನು ಭಾಗಿಸಬೇಕು. ಒಂದು ಉದಾಹರಣೆಯೊಂದಿಗೆ ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿ ವ್ಯಾಖ್ಯಾನವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳೋಣ.

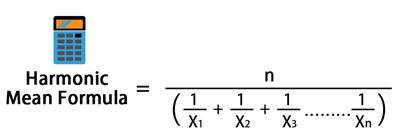
1, 3, 5, ಮತ್ತು 10 ರ ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನಿಮ್ಮನ್ನು ಕೇಳಲಾಗಿದೆ ಎಂದು ಭಾವಿಸೋಣ. ಈಗ ನೀವು ಒಟ್ಟು 4 ವೀಕ್ಷಣೆಗಳನ್ನು ಹೊಂದಿದ್ದೀರಿ, ನೀವು 4 ಅನ್ನು ಪ್ರತಿ ಸಂಖ್ಯೆಯ ಪರಸ್ಪರ ಮೊತ್ತದಿಂದ ಭಾಗಿಸುತ್ತೀರಿ, ಅಂದರೆ 1/1 + 1/3 + 1/5 + 1/10. ಈ ಪ್ರತಿಸ್ಪರ್ಧಿಗಳ ಮೊತ್ತದಿಂದ ನೀವು ಪಡೆಯುವ ಒಟ್ಟು ಮೊತ್ತವನ್ನು 4 ರಿಂದ ಭಾಗಿಸಿದಾಗ, ಈ ಲೆಕ್ಕಾಚಾರದ ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿಯನ್ನು ನೀವು ಪಡೆಯುತ್ತೀರಿ.

ಹಾರ್ಮೋನಿಕ್ ಮೀನ್‌ನ ಅವಲೋಕನ

ಸಬ್‌ಕಾಂಟ್ರರಿ ಮೀನ್ ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ, ನೀಡಿರುವ ಅಂಕಿಗಳ ಸರಾಸರಿಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಹಾರ್ಮೋನಿಕ್ ಮೀನ್ ಅನ್ನು ಸಾಮಾನ್ಯ ಲೆಕ್ಕಾಚಾರದ ಆಯ್ಕೆಯಾಗಿ ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ. ಹಾರ್ಮೋನಿಕ್ ಮೀನ್ ಕಾನ್ಕೇವ್ ಆಗಿರುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸುವುದು ಮುಖ್ಯ. ಇದನ್ನು ಹೇಳುವುದರೊಂದಿಗೆ, ಸರಾಸರಿಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನೀವು ಬಳಸುವ ಸಂಖ್ಯೆಗಳಿಗೆ ನೀವು ವಿಶೇಷ ಗಮನ ಹರಿಸಬೇಕು. ಇಲ್ಲಿ, ನೀವು ಋಣಾತ್ಮಕ ಸಂಖ್ಯೆಗಳನ್ನು ಬಳಸಲಾಗುವುದಿಲ್ಲ.

ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿಯು ಪೈಥಾಗರಿಯನ್ ಸರಾಸರಿಯ ಒಂದು ಭಾಗವಾಗಿದೆ, ಇದು ಒಟ್ಟು ಮೂರು ವಿಧಾನಗಳನ್ನು ಒಳಗೊಂಡಿದೆ (ಮೊದಲ ಮತ್ತು ಎರಡನೆಯದು ಕ್ರಮವಾಗಿ ಅಂಕಗಣಿತದ ಸರಾಸರಿ ಮತ್ತು ಜ್ಯಾಮಿತೀಯ ಸರಾಸರಿ). ಕೊಟ್ಟಿರುವ ಮೌಲ್ಯಗಳು ಒಂದೇ ಆಗಿದ್ದರೆ ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿಯು ಅಂಕಗಣಿತ ಮತ್ತು ಜ್ಯಾಮಿತೀಯ ಸರಾಸರಿಯಂತೆಯೇ ಇರುತ್ತದೆ.

ಉದಾಹರಣೆಗೆ, ನೀಡಲಾದ ಮೌಲ್ಯಗಳು 4, 4 ಮತ್ತು 4 ಆಗಿದ್ದರೆ ಎಲ್ಲಾ ಮೂರು ಪೈಥಾಗರಿಯನ್ ಅರ್ಥಗಳು 4 ಆಗಿರುತ್ತದೆ. ಅಂಕಗಣಿತದ ಸರಾಸರಿಯು ಸಾಮಾನ್ಯವಾಗಿ ಬಳಸಲ್ಪಡುವುದರಿಂದ, ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿಯು ಅಂಕಗಣಿತದ ಸರಾಸರಿಯೊಂದಿಗೆ ಹೆಚ್ಚಾಗಿ ಗೊಂದಲಕ್ಕೊಳಗಾಗುತ್ತದೆ. ಅನೇಕ ಸ್ಥಳಗಳಲ್ಲಿ, ಹಾರ್ಮೋನಿಕ್ ಎಂದರೆ ಅತ್ಯುತ್ತಮವಾದ ಸರಾಸರಿಯನ್ನು ನೀಡುತ್ತದೆ. ನೀಡಿರುವ ಮೌಲ್ಯವನ್ನು ಅನುಪಾತಗಳು ಮತ್ತು ದರಗಳಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಿದಾಗ ಸರಾಸರಿ ಲೆಕ್ಕಾಚಾರಕ್ಕೆ ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿಯನ್ನು ಮುಖ್ಯವಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ.

ಅಂಕಗಣಿತ ಮತ್ತು ಹಾರ್ಮೋನಿಕ್ ವಿಧಾನಗಳನ್ನು ಎಲ್ಲಿ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ನಾವು ಇನ್ನೊಂದು ಉದಾಹರಣೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ.

ಹಾರ್ಮೋನಿಕ್ ಮೀನ್ Vs ಅಂಕಗಣಿತದ ಸರಾಸರಿ

ಉದಾಹರಣೆಗೆ, ವಾಹನದ ವೇಗ ಮತ್ತು ಅದರ ದೂರವನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ. ರೈಲು ನಿರ್ದಿಷ್ಟ ವೇಗದಲ್ಲಿ ಪ್ರಯಾಣಿಸುವ ನಿರ್ದಿಷ್ಟ ದೂರವನ್ನು ಕ್ರಮಿಸಿದೆ ಎಂದು ಹೇಳೋಣ. ಈಗ, ಹಿಂತಿರುಗುವಾಗ ಅದೇ ದೂರವನ್ನು ಅದು ಆವರಿಸಿದರೆ, ನಂತರ ರೈಲಿನ ಸರಾಸರಿ ವೇಗವನ್ನು ಹಾರ್ಮೋನಿಕ್ ಸರಾಸರಿ ಬಳಸಿ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. ಈ ಗಣಿತದ ಸೂತ್ರವು ರೈಲು ಗಮ್ಯಸ್ಥಾನಕ್ಕೆ ಮರಳಬೇಕಾದ ಸರಾಸರಿ ವೇಗವನ್ನು ಕಂಡುಹಿಡಿಯಲು ನಿಮಗೆ ಸಹಾಯ ಮಾಡುತ್ತದೆ. ಈ ರೈಲು ವಿಭಿನ್ನ ವೇಗದಲ್ಲಿ ಚಲಿಸಿದರೆ ಗಮ್ಯಸ್ಥಾನವನ್ನು ತಲುಪಲು ಸಮಾನ ಸಮಯವನ್ನು ತೆಗೆದುಕೊಂಡರೆ, ರೈಲಿನ ಸರಾಸರಿ ವೇಗವನ್ನು ಪಡೆಯಲು ನೀವು ಅಂಕಗಣಿತದ ಸರಾಸರಿಯನ್ನು ಲೆಕ್ಕ ಹಾಕಬೇಕಾಗುತ್ತದೆ.

ಅದೇ ಉದಾಹರಣೆಯು ಪ್ರತಿ ಲೆಕ್ಕಾಚಾರಕ್ಕೂ ಅನ್ವಯಿಸುತ್ತದೆ, ಇದರಲ್ಲಿ ಬಳಕೆದಾರರು ಪ್ರಯಾಣಿಸಿದ ದೂರವನ್ನು ನೀಡಿದ ವಾಹನದ ಸರಾಸರಿ ವೇಗವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಪ್ರಯತ್ನಿಸುತ್ತಾರೆ. ನಿಮ್ಮ ವಾಹನವು ಒಂದೇ ದೂರವನ್ನು ವಿಭಿನ್ನ ವೇಗದಲ್ಲಿ ಕ್ರಮಿಸಿದರೆ, ವಾಹನದ ಸರಾಸರಿ ವೇಗವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನೀವು ಹಾರ್ಮೋನಿಕ್ ಮೀನ್ ಅನ್ನು ಬಳಸಬೇಕಾಗುತ್ತದೆ.