ഹാർമോണിക് ശരാശരി

എന്താണ് ഹാർമോണിക് അർത്ഥം?

നൽകിയിരിക്കുന്ന കണക്കുകളുടെ ഹാർമോണിക് ശരാശരി കണക്കാക്കാൻ, നിങ്ങൾ നിരീക്ഷണങ്ങളുടെ ആകെ എണ്ണം ഓരോ സംഖ്യയുടെയും പരസ്പരവിരുദ്ധമായി ഹരിക്കേണ്ടതുണ്ട്. ഒരു ഉദാഹരണത്തിലൂടെ നമുക്ക് ഹാർമോണിക് ശരാശരി നിർവചനം മനസ്സിലാക്കാം.

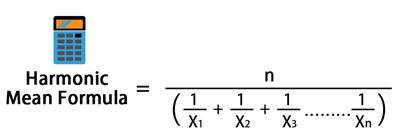
1, 3, 5, 10 എന്നിവയുടെ ഹാർമോണിക് ശരാശരി കണക്കാക്കാൻ നിങ്ങളോട് ആവശ്യപ്പെട്ടുവെന്നിരിക്കട്ടെ. ഇപ്പോൾ നിങ്ങൾക്ക് ആകെ 4 നിരീക്ഷണങ്ങളുണ്ട്, നിങ്ങൾ 4 നെ ഓരോ സംഖ്യയുടെയും പരസ്പരമുള്ള തുകകൊണ്ട് ഹരിക്കും, അതായത് 1/1 + 1/3 + 1/5 + 1/10. ഈ റെസിപ്രോക്കലുകളുടെ ആകെത്തുകയിൽ നിന്ന് നിങ്ങൾക്ക് ലഭിക്കുന്ന മൊത്തത്തെ 4 കൊണ്ട് ഹരിച്ചാൽ, ഈ കണക്കുകൂട്ടലിന്റെ ഹാർമോണിക് ശരാശരി നിങ്ങൾക്ക് ലഭിക്കും.

ഹാർമോണിക് മീനിന്റെ ഒരു അവലോകനം

ഉപവിരുദ്ധ ശരാശരി എന്നും അറിയപ്പെടുന്നു, നൽകിയിരിക്കുന്ന കണക്കുകളുടെ ശരാശരി കണക്കാക്കുന്നതിനുള്ള ഒരു സാധാരണ കണക്കുകൂട്ടൽ ഓപ്ഷനായി ഹാർമോണിക് ശരാശരി കണക്കാക്കപ്പെടുന്നു. ഹാർമോണിക് മീഡിയൻ കോൺകേവ് ആയിരിക്കുമെന്നത് ശ്രദ്ധിക്കേണ്ടതാണ്. അങ്ങനെ പറയുമ്പോൾ, ശരാശരി കണക്കാക്കാൻ നിങ്ങൾ ഉപയോഗിക്കുന്ന സംഖ്യകളിൽ നിങ്ങൾ പ്രത്യേകം ശ്രദ്ധിക്കേണ്ടതുണ്ട്. ഇവിടെ, നിങ്ങൾക്ക് നെഗറ്റീവ് നമ്പറുകൾ ഉപയോഗിക്കാൻ കഴിയില്ല.

പൈതഗോറിയൻ ശരാശരിയുടെ ഒരു ഭാഗമാണ് ഹാർമോണിക് ശരാശരി, അതിൽ ആകെ മൂന്ന് മാർഗങ്ങൾ അടങ്ങിയിരിക്കുന്നു (ആദ്യത്തേതും രണ്ടാമത്തേതും യഥാക്രമം ഗണിത ശരാശരിയും ജ്യാമിതീയ ശരാശരിയുമാണ്). നൽകിയിരിക്കുന്ന മൂല്യങ്ങൾ ഒന്നുതന്നെയാണെങ്കിൽ, ഹാർമോണിക് ശരാശരിയും ഗണിതവും ജ്യാമിതീയവും തുല്യമായിരിക്കും.

ഉദാഹരണത്തിന്, നൽകിയിരിക്കുന്ന മൂല്യങ്ങൾ 4, 4, 4 എന്നിവയാണെങ്കിൽ മൂന്ന് പൈതഗോറിയൻ മാർഗങ്ങളും 4 ആയിരിക്കും. ഗണിത ശരാശരി വളരെ സാധാരണയായി ഉപയോഗിക്കുന്നതിനാൽ, ഹാർമോണിക് ശരാശരിയെ ഗണിത ശരാശരിയുമായി ആശയക്കുഴപ്പത്തിലാക്കുന്നു. പലയിടത്തും, ഹാർമോണിക് മാർഗങ്ങൾ ഏറ്റവും മികച്ച ശരാശരി നൽകുന്നു. നൽകിയിരിക്കുന്ന മൂല്യം അനുപാതങ്ങളിലും നിരക്കുകളിലും പ്രകടിപ്പിക്കുമ്പോൾ ശരാശരിയുടെ കണക്കുകൂട്ടലിനായി ഹാർമോണിക് ശരാശരിയാണ് പ്രധാനമായും ഉപയോഗിക്കുന്നത്.

ഗണിതവും ഹാർമോണിക് മാർഗങ്ങളും എവിടെയാണ് കണക്കാക്കുന്നതെന്ന് മനസിലാക്കാൻ ഞങ്ങൾ മറ്റൊരു ഉദാഹരണം എടുക്കാൻ പോകുന്നു.

ഹാർമോണിക് മീൻ Vs അരിത്മെറ്റിക് മീൻ

ഉദാഹരണത്തിന്, വാഹനത്തിന്റെ വേഗതയും അതിന്റെ ദൂരവും എടുക്കുക. ഒരു ട്രെയിൻ ഒരു പ്രത്യേക വേഗതയിൽ സഞ്ചരിക്കുന്ന ഒരു നിശ്ചിത ദൂരം പിന്നിട്ടിട്ടുണ്ടെന്ന് പറയാം. ഇപ്പോൾ, തിരികെ വരുമ്പോൾ അതേ ദൂരം അത് ഉൾക്കൊള്ളുന്നുവെങ്കിൽ, ട്രെയിനിന്റെ ശരാശരി വേഗത ഹാർമോണിക് ശരാശരി ഉപയോഗിച്ച് കണക്കാക്കും. ഈ ഗണിത സൂത്രവാക്യം ട്രെയിൻ ലക്ഷ്യസ്ഥാനത്ത് തിരിച്ചെത്തിയിരിക്കേണ്ട ശരാശരി വേഗത കണ്ടെത്താൻ നിങ്ങളെ സഹായിക്കും. ഈ ട്രെയിൻ വ്യത്യസ്ത വേഗതയിൽ സഞ്ചരിക്കുന്നുണ്ടെങ്കിലും ലക്ഷ്യസ്ഥാനത്ത് എത്താൻ തുല്യ സമയമെടുക്കുകയാണെങ്കിൽ, ട്രെയിനിന്റെ ശരാശരി വേഗത ലഭിക്കുന്നതിന് നിങ്ങൾ ഗണിത ശരാശരി കണക്കാക്കേണ്ടതുണ്ട്.

ഓരോ കണക്കുകൂട്ടലിനും ഇതേ ഉദാഹരണം ബാധകമാണ്, അതിൽ യാത്ര ചെയ്ത ദൂരം നൽകിയിട്ടുള്ള വാഹനത്തിന്റെ ശരാശരി വേഗത കണ്ടെത്താൻ ഉപയോക്താവ് ശ്രമിക്കുന്നു. നിങ്ങളുടെ വാഹനം ഒരേ ദൂരം വ്യത്യസ്ത വേഗതയിൽ സഞ്ചരിക്കുകയാണെങ്കിൽ, വാഹനത്തിന്റെ ശരാശരി വേഗത കണക്കാക്കാൻ നിങ്ങൾ ഹാർമോണിക് മീഡിയം ഉപയോഗിക്കേണ്ടതുണ്ട്.