हार्मोनिक मीन

हार्मोनिक म्हणजे काय?

दिलेल्या आकृत्यांच्या हार्मोनिक मध्याची गणना करण्यासाठी, तुम्हाला प्रत्येक संख्येच्या परस्परसंख्येने एकूण निरीक्षणांची संख्या भागली पाहिजे. उदाहरणासह हार्मोनिक मीन व्याख्या समजून घेऊ.

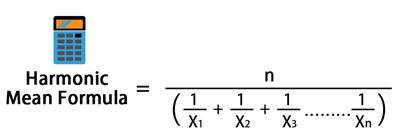
समजा तुम्हाला 1, 3, 5 आणि 10 चा हार्मोनिक मीन काढण्यास सांगितले आहे. आता तुमच्याकडे एकूण 4 निरीक्षणे आहेत, तुम्ही प्रत्येक संख्येच्या परस्परसंख्येच्या बेरजेने 4 ला भागणार आहात, म्हणजे 1/1 + 1/3 + १/५ + १/१०. या परस्परसंख्येच्या बेरजेतून तुम्हाला मिळणार्‍या एकूण रकमेला ४ ने भागल्यावर, तुम्हाला या गणनेचा हार्मोनिक सरासरी मिळेल.

हार्मोनिक मीनचे विहंगावलोकन

उपकंट्रारी मीन म्हणूनही ओळखले जाते, दिलेल्‍या आकृत्यांची सरासरी काढण्‍यासाठी हार्मोनिक माध्‍यक हा एक सामान्य गणना पर्याय मानला जातो. हे लक्षात घेणे महत्वाचे आहे की हार्मोनिक मीन अवतल असतो. असे म्हटल्याप्रमाणे, आपण सरासरी मोजण्यासाठी वापरत असलेल्या संख्येकडे विशेष लक्ष देणे आवश्यक आहे. येथे, तुम्ही ऋण संख्या वापरू शकत नाही.

हार्मोनिक मीन हा पायथागोरियन मीनचा एक भाग आहे, ज्यामध्ये एकूण तीन माध्यमे असतात (पहिला आणि दुसरा म्हणजे अनुक्रमे अंकगणितीय माध्य आणि भौमितिक माध्य). दिलेली मूल्ये समान असल्यास हार्मोनिक माध्य अंकगणित आणि भूमितीय माध्य सारखा असेल.

उदाहरणार्थ, दिलेली मूल्ये 4, 4 आणि 4 असल्यास, तीनही पायथागोरियन अर्थ 4 असतील. अंकगणितीय सरासरीचा सामान्यतः वापर केला जात असल्याने, हार्मोनिक मीन बहुतेक वेळा अंकगणितीय मध्याशी गोंधळलेला असतो. बर्‍याच ठिकाणी, हार्मोनिक म्हणजे सर्वोत्तम संभाव्य सरासरी देतात. लक्षात ठेवा जेव्हा दिलेले मूल्य गुणोत्तर आणि दरांमध्ये व्यक्त केले जाते तेव्हा हार्मोनिक मीन प्रामुख्याने सरासरीच्या गणनेसाठी वापरले जाते.

अंकगणित आणि हार्मोनिक माध्यमांची गणना कुठे केली जाते हे समजून घेण्यासाठी आपण आणखी एक उदाहरण घेणार आहोत.

हार्मोनिक मीन वि अंकगणित मीन

उदाहरणार्थ, वाहनाचा वेग आणि त्याचे अंतर घ्या. समजा ट्रेनने विशिष्ट वेगाने प्रवास करत एक विशिष्ट अंतर कापले आहे. आता परत येताना तेच अंतर कापले तर हार्मोनिक मीन वापरून ट्रेनचा सरासरी वेग काढला जाईल. हे गणितीय सूत्र तुम्हाला ट्रेन गंतव्यस्थानी परतली असावी असा सरासरी वेग शोधण्यात मदत करेल. जर ही ट्रेन वेगवेगळ्या वेगाने प्रवास करत असेल तरीही गंतव्यस्थानावर पोहोचण्यासाठी समान वेळ घेत असेल, तर तुम्हाला ट्रेनचा सरासरी वेग मिळवण्यासाठी अंकगणित सरासरी काढावी लागेल.

हेच उदाहरण प्रत्येक गणनेला लागू होते, ज्यामध्ये वापरकर्ता प्रवास केलेले अंतर लक्षात घेऊन वाहनाचा सरासरी वेग काढण्याचा प्रयत्न करतो. जर तुमचे वाहन समान अंतर वेगवेगळ्या वेगाने कापत असेल, तर तुम्हाला वाहनाच्या सरासरी वेगाची गणना करण्यासाठी हार्मोनिक मीन वापरावे लागेल.