ਹਾਰਮੋਨਿਕ ਮੀਨ

ਹਾਰਮੋਨਿਕ ਦਾ ਮਤਲਬ ਕੀ ਹੈ?

ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਦੇ ਹਾਰਮੋਨਿਕ ਮਾਧਿਅਮ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ, ਤੁਹਾਨੂੰ ਹਰੇਕ ਸੰਖਿਆ ਦੇ ਪਰਸਪਰ ਸੰਖਿਆ ਦੁਆਰਾ ਨਿਰੀਖਣਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ ਨੂੰ ਵੰਡਣਾ ਚਾਹੀਦਾ ਹੈ। ਆਉ ਇੱਕ ਉਦਾਹਰਨ ਦੇ ਨਾਲ ਹਾਰਮੋਨਿਕ ਅਰਥ ਪਰਿਭਾਸ਼ਾ ਨੂੰ ਸਮਝੀਏ।

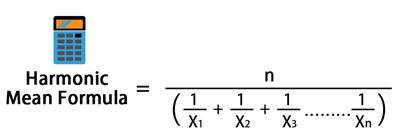
ਮੰਨ ਲਓ ਕਿ ਤੁਹਾਨੂੰ 1, 3, 5 ਅਤੇ 10 ਦੇ ਹਾਰਮੋਨਿਕ ਮਾਧਿਅਮ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ ਕਿਹਾ ਗਿਆ ਹੈ। ਹੁਣ ਜਦੋਂ ਤੁਹਾਡੇ ਕੋਲ ਕੁੱਲ 4 ਨਿਰੀਖਣ ਹਨ, ਤੁਸੀਂ 4 ਨੂੰ ਹਰੇਕ ਸੰਖਿਆ ਦੇ ਪਰਸਪਰ ਸੰਖਿਆ ਦੇ ਜੋੜ ਨਾਲ ਭਾਗ ਕਰ ਰਹੇ ਹੋਵੋਗੇ, ਭਾਵ 1/1 + 1/3 + 1/5 + 1/10। ਇਹਨਾਂ ਪਰਿਵਰਤਨਾਂ ਦੇ ਜੋੜ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਏ ਕੁੱਲ ਨੂੰ 4 ਨਾਲ ਵੰਡਣ 'ਤੇ, ਤੁਹਾਨੂੰ ਇਸ ਗਣਨਾ ਦਾ ਹਾਰਮੋਨਿਕ ਮਾਧਿਅਮ ਮਿਲੇਗਾ।

ਹਾਰਮੋਨਿਕ ਮੀਨ ਦੀ ਇੱਕ ਸੰਖੇਪ ਜਾਣਕਾਰੀ

ਉਪ-ਵਿਰੋਧੀ ਮੱਧਮਾਨ ਵਜੋਂ ਵੀ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ, ਹਾਰਮੋਨਿਕ ਮੱਧਮਾਨ ਨੂੰ ਦਿੱਤੇ ਅੰਕੜਿਆਂ ਦੀ ਔਸਤ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ ਇੱਕ ਆਮ ਗਣਨਾ ਵਿਕਲਪ ਵਜੋਂ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ। ਇਹ ਨੋਟ ਕਰਨਾ ਮਹੱਤਵਪੂਰਨ ਹੈ ਕਿ ਹਾਰਮੋਨਿਕ ਮਾਧਿਅਮ ਅਵਤਲ ਹੁੰਦਾ ਹੈ। ਇਹ ਕਿਹਾ ਜਾ ਰਿਹਾ ਹੈ, ਤੁਹਾਨੂੰ ਔਸਤ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ ਤੁਹਾਡੇ ਦੁਆਰਾ ਵਰਤੇ ਗਏ ਸੰਖਿਆਵਾਂ 'ਤੇ ਵਿਸ਼ੇਸ਼ ਧਿਆਨ ਦੇਣ ਦੀ ਲੋੜ ਹੈ। ਇੱਥੇ, ਤੁਸੀਂ ਨਕਾਰਾਤਮਕ ਸੰਖਿਆਵਾਂ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰ ਸਕਦੇ ਹੋ।

ਹਾਰਮੋਨਿਕ ਮੱਧਮਾਨ ਪਾਇਥਾਗੋਰਿਅਨ ਮਾਧਿਅਮ ਦਾ ਇੱਕ ਹਿੱਸਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਕੁੱਲ ਤਿੰਨ ਸਾਧਨ ਹੁੰਦੇ ਹਨ (ਪਹਿਲਾ ਅਤੇ ਦੂਜਾ ਕ੍ਰਮਵਾਰ ਗਣਿਤ ਦਾ ਮਤਲਬ ਅਤੇ ਜਿਓਮੈਟ੍ਰਿਕ ਮਤਲਬ)। ਹਾਰਮੋਨਿਕ ਮੱਧਮਾਨ ਅੰਕਗਣਿਤ ਅਤੇ ਜਿਓਮੈਟ੍ਰਿਕ ਮਾਧਿਅਮ ਦੇ ਸਮਾਨ ਹੋਵੇਗਾ ਜੇਕਰ ਦਿੱਤੇ ਗਏ ਮੁੱਲ ਇੱਕੋ ਹਨ।

ਉਦਾਹਰਨ ਲਈ, ਸਾਰੇ ਤਿੰਨ ਪਾਇਥਾਗੋਰਿਅਨ ਮਤਲਬ 4 ਹੋਣਗੇ ਜੇਕਰ ਦਿੱਤੇ ਗਏ ਮੁੱਲ 4, 4, ਅਤੇ 4 ਹਨ। ਕਿਉਂਕਿ ਗਣਿਤ ਦਾ ਮਤਲਬ ਆਮ ਤੌਰ 'ਤੇ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ, ਹਾਰਮੋਨਿਕ ਮੱਧਮਾਨ ਅਕਸਰ ਗਣਿਤ ਦੇ ਮੱਧਮਾਨ ਨਾਲ ਉਲਝਿਆ ਹੁੰਦਾ ਹੈ। ਬਹੁਤ ਸਾਰੀਆਂ ਥਾਵਾਂ 'ਤੇ, ਹਾਰਮੋਨਿਕ ਸਾਧਨ ਸਭ ਤੋਂ ਵਧੀਆ ਸੰਭਵ ਔਸਤ ਦਿੰਦੇ ਹਨ। ਨੋਟ ਕਰੋ ਕਿ ਹਾਰਮੋਨਿਕ ਮਾਧਿਅਮ ਮੁੱਖ ਤੌਰ 'ਤੇ ਔਸਤ ਦੀ ਗਣਨਾ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ਜਦੋਂ ਦਿੱਤੇ ਮੁੱਲ ਨੂੰ ਅਨੁਪਾਤ ਅਤੇ ਦਰਾਂ ਵਿੱਚ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ।

ਅਸੀਂ ਇਹ ਸਮਝਣ ਲਈ ਇੱਕ ਹੋਰ ਉਦਾਹਰਣ ਲੈਣ ਜਾ ਰਹੇ ਹਾਂ ਕਿ ਗਣਿਤ ਅਤੇ ਹਾਰਮੋਨਿਕ ਸਾਧਨਾਂ ਦੀ ਗਣਨਾ ਕਿੱਥੇ ਕੀਤੀ ਜਾਂਦੀ ਹੈ।

ਹਾਰਮੋਨਿਕ ਮੀਨ ਬਨਾਮ ਅੰਕਗਣਿਤ ਦਾ ਮਤਲਬ

ਉਦਾਹਰਨ ਲਈ, ਵਾਹਨ ਦੀ ਗਤੀ ਅਤੇ ਇਸਦੀ ਦੂਰੀ ਨੂੰ ਲਓ। ਮੰਨ ਲਓ ਕਿ ਇੱਕ ਰੇਲਗੱਡੀ ਨੇ ਇੱਕ ਖਾਸ ਸਪੀਡ 'ਤੇ ਯਾਤਰਾ ਕਰਦੇ ਹੋਏ ਇੱਕ ਖਾਸ ਦੂਰੀ ਨੂੰ ਪੂਰਾ ਕੀਤਾ ਹੈ। ਹੁਣ, ਜੇਕਰ ਇਹ ਵਾਪਸੀ ਵੇਲੇ ਉਹੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ, ਤਾਂ ਹਾਰਮੋਨਿਕ ਮਾਧਿਅਮ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਗਤੀ ਦੀ ਗਣਨਾ ਕੀਤੀ ਜਾਵੇਗੀ। ਇਹ ਗਣਿਤਿਕ ਫਾਰਮੂਲਾ ਤੁਹਾਨੂੰ ਔਸਤ ਗਤੀ ਦਾ ਪਤਾ ਲਗਾਉਣ ਵਿੱਚ ਮਦਦ ਕਰੇਗਾ ਜਿਸ ਨਾਲ ਟ੍ਰੇਨ ਮੰਜ਼ਿਲ 'ਤੇ ਵਾਪਸ ਆਈ ਹੋਵੇਗੀ। ਜੇਕਰ ਇਹ ਰੇਲਗੱਡੀ ਵੱਖ-ਵੱਖ ਰਫ਼ਤਾਰਾਂ 'ਤੇ ਸਫ਼ਰ ਕਰਦੀ ਹੈ ਪਰ ਮੰਜ਼ਿਲ 'ਤੇ ਪਹੁੰਚਣ ਲਈ ਬਰਾਬਰ ਸਮਾਂ ਲੈਂਦੀ ਹੈ, ਤਾਂ ਤੁਹਾਨੂੰ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਗਤੀ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਗਣਿਤ ਦੇ ਮਾਧਿਅਮ ਦੀ ਗਣਨਾ ਕਰਨ ਦੀ ਲੋੜ ਹੋਵੇਗੀ।

ਇਹੀ ਉਦਾਹਰਨ ਹਰ ਗਣਨਾ 'ਤੇ ਲਾਗੂ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਵਿੱਚ ਉਪਭੋਗਤਾ ਦੂਰੀ ਦੀ ਸਫ਼ਰ ਕਰਨ ਦੇ ਮੱਦੇਨਜ਼ਰ ਵਾਹਨ ਦੀ ਔਸਤ ਗਤੀ ਦਾ ਪਤਾ ਲਗਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ। ਜੇਕਰ ਤੁਹਾਡਾ ਵਾਹਨ ਵੱਖ-ਵੱਖ ਗਤੀ 'ਤੇ ਇੱਕੋ ਦੂਰੀ ਨੂੰ ਪੂਰਾ ਕਰਦਾ ਹੈ, ਤਾਂ ਤੁਹਾਨੂੰ ਵਾਹਨ ਦੀ ਔਸਤ ਗਤੀ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ ਹਾਰਮੋਨਿਕ ਮਾਧਿਅਮ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦੀ ਲੋੜ ਹੈ।