Table of Contents

ஹார்மோனிக் சராசரி

Updated on November 4, 2024 , 7315 views

ஹார்மோனிக் அர்த்தம் என்ன?

கொடுக்கப்பட்ட புள்ளிவிவரங்களின் ஒத்திசைவான சராசரியைக் கணக்கிட, நீங்கள் ஒவ்வொரு எண்ணின் பரஸ்பரம் மூலம் அவதானிப்புகளின் மொத்த எண்ணிக்கையை வகுக்க வேண்டும். ஒரு எடுத்துக்காட்டுடன் ஹார்மோனிக் சராசரி வரையறையைப் புரிந்துகொள்வோம்.

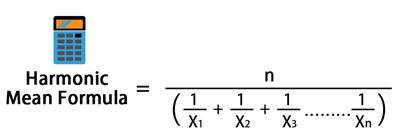
1, 3, 5, மற்றும் 10 ஆகியவற்றின் ஹார்மோனிக் சராசரியைக் கணக்கிடும்படி உங்களிடம் கேட்கப்பட்டதாக வைத்துக் கொள்வோம். இப்போது உங்களிடம் மொத்தம் 4 அவதானிப்புகள் இருப்பதால், நீங்கள் 4 ஐ ஒவ்வொரு எண்ணின் பரஸ்பரத்தின் கூட்டுத்தொகையால் வகுக்க வேண்டும், அதாவது 1/1 + 1/3 + 1/5 + 1/10. இந்த எதிரொலிகளின் கூட்டுத்தொகையிலிருந்து நீங்கள் பெறும் மொத்தத்தை 4 ஆல் வகுத்தால், இந்தக் கணக்கீட்டின் ஒத்திசைவான சராசரியைப் பெறுவீர்கள்.

ஹார்மோனிக் மீனின் கண்ணோட்டம்

சப்கான்ட்ராரி சராசரி என்றும் அறியப்படும், கொடுக்கப்பட்ட புள்ளிவிவரங்களின் சராசரியைக் கணக்கிடுவதற்கான பொதுவான கணக்கீட்டு விருப்பமாக ஹார்மோனிக் சராசரி கருதப்படுகிறது. ஹார்மோனிக் சராசரி குழிவானதாக இருக்கும் என்பதை கவனத்தில் கொள்ள வேண்டும். இதைச் சொல்லும்போது, சராசரியைக் கணக்கிட நீங்கள் பயன்படுத்தும் எண்களுக்கு சிறப்பு கவனம் செலுத்த வேண்டும். இங்கே, நீங்கள் எதிர்மறை எண்களைப் பயன்படுத்த முடியாது.

ஹார்மோனிக் சராசரி என்பது பித்தகோரியன் சராசரியின் ஒரு பகுதியாகும், இது மொத்தம் மூன்று வழிமுறைகளைக் கொண்டுள்ளது (முதல் மற்றும் இரண்டாவது முறையே எண்கணித சராசரி மற்றும் வடிவியல் சராசரி). கொடுக்கப்பட்ட மதிப்புகள் ஒரே மாதிரியாக இருந்தால், ஹார்மோனிக் சராசரி எண்கணிதம் மற்றும் வடிவியல் சராசரியாக இருக்கும்.

எடுத்துக்காட்டாக, கொடுக்கப்பட்ட மதிப்புகள் 4, 4 மற்றும் 4 என இருந்தால் மூன்று பித்தகோரியன் வழிமுறைகளும் 4 ஆக இருக்கும். எண்கணித சராசரி பொதுவாகப் பயன்படுத்தப்படுவதால், ஹார்மோனிக் சராசரியானது எண்கணித சராசரியுடன் அடிக்கடி குழப்பமடைகிறது. பல இடங்களில், ஹார்மோனிக் என்பது சிறந்த சராசரியை அளிக்கிறது. கொடுக்கப்பட்ட மதிப்பு விகிதங்கள் மற்றும் விகிதங்களில் வெளிப்படுத்தப்படும்போது சராசரியைக் கணக்கிடுவதற்கு ஹார்மோனிக் சராசரி முக்கியமாகப் பயன்படுத்தப்படுகிறது என்பதை நினைவில் கொள்க.

எண்கணிதம் மற்றும் ஹார்மோனிக் வழிமுறைகள் எங்கு கணக்கிடப்படுகின்றன என்பதைப் புரிந்துகொள்ள மற்றொரு உதாரணத்தை எடுக்கப் போகிறோம்.

Ready to Invest?
Talk to our investment specialist

ஹார்மோனிக் சராசரி Vs எண்கணித சராசரி

உதாரணமாக, வாகனத்தின் வேகம் மற்றும் அதன் தூரத்தை எடுத்துக் கொள்ளுங்கள். ஒரு ரயில் குறிப்பிட்ட தூரத்தை குறிப்பிட்ட வேகத்தில் கடந்து சென்றதாக வைத்துக் கொள்வோம். இப்போது, திரும்பும் போது அதே தூரத்தை அது கடந்தால், ரயிலின் சராசரி வேகம் ஹார்மோனிக் சராசரியைப் பயன்படுத்தி கணக்கிடப்படும். இந்த கணித சூத்திரம் ரயில் இலக்குக்கு திரும்பியிருக்க வேண்டிய சராசரி வேகத்தைக் கண்டறிய உதவும். இந்த ரயில் வெவ்வேறு வேகத்தில் பயணித்து, இலக்கை அடைய சமமான நேரத்தை எடுத்துக் கொண்டால், ரயிலின் சராசரி வேகத்தைப் பெற, நீங்கள் எண்கணித சராசரியைக் கணக்கிட வேண்டும்.

ஒவ்வொரு கணக்கீட்டிற்கும் இதே உதாரணம் பொருந்தும், இதில் பயணித்த தூரம் கொடுக்கப்பட்ட வாகனத்தின் சராசரி வேகத்தைக் கண்டுபிடிக்க பயனர் முயற்சி செய்கிறார். உங்கள் வாகனம் ஒரே தூரத்தை வெவ்வேறு வேகத்தில் சென்றால், வாகனத்தின் சராசரி வேகத்தைக் கணக்கிட நீங்கள் ஹார்மோனிக் சராசரியைப் பயன்படுத்த வேண்டும்.

Disclaimer:
இங்கு வழங்கப்பட்ட தகவல்கள் துல்லியமானவை என்பதை உறுதிப்படுத்த அனைத்து முயற்சிகளும் மேற்கொள்ளப்பட்டுள்ளன. இருப்பினும், தரவின் சரியான தன்மை குறித்து எந்த உத்தரவாதமும் அளிக்கப்படவில்லை. முதலீடு செய்வதற்கு முன் திட்டத் தகவல் ஆவணத்துடன் சரிபார்க்கவும்.