ہارمونک مطلب

ہارمونک کا مطلب کیا ہے؟

دیے گئے اعداد و شمار کے ہارمونک وسط کا حساب لگانے کے لیے، آپ کو مشاہدات کی کل تعداد کو ہر نمبر کے باہم سے تقسیم کرنا ہوگا۔ آئیے ایک مثال کے ساتھ ہارمونک مطلب کی تعریف کو سمجھیں۔

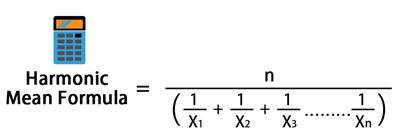
فرض کریں کہ آپ سے 1، 3، 5 اور 10 کے ہارمونک اوسط کا حساب لگانے کے لیے کہا گیا ہے۔ اب جب کہ آپ کے پاس کل 4 مشاہدات ہیں، آپ 4 کو ہر ایک عدد کے بامقابل کے مجموعہ سے تقسیم کر رہے ہوں گے، یعنی 1/1 + 1/3 + 1/5 + 1/10۔ ان ریپروکلز کے مجموعے سے حاصل ہونے والے کل کو 4 سے تقسیم کرنے پر، آپ کو اس حساب کا ہارمونک اوسط ملے گا۔

ہارمونک مین کا ایک جائزہ

ذیلی متضاد وسط کے طور پر بھی جانا جاتا ہے، ہارمونک وسط کو دیے گئے اعداد و شمار کی اوسط کا حساب لگانے کے لیے ایک عام حساب کے اختیار کے طور پر سمجھا جاتا ہے۔ یہ نوٹ کرنا ضروری ہے کہ ہارمونک مطلب مقعر ہوتا ہے۔ یہ کہنے کے ساتھ، آپ کو ان نمبروں پر خصوصی توجہ دینے کی ضرورت ہے جو آپ اوسط کا حساب لگانے کے لیے استعمال کرتے ہیں۔ یہاں، آپ منفی نمبر استعمال نہیں کر سکتے۔

ہارمونک وسط Pythagorean اوسط کا ایک حصہ ہے، جو کل تین ذرائع پر مشتمل ہے (پہلا اور دوسرا بالترتیب ریاضی کا مطلب اور ہندسی مطلب ہے)۔ اگر دی گئی قدریں یکساں ہوں تو ہارمونک وسط ریاضی اور جیومیٹرک وسط جیسا ہی ہوگا۔

مثال کے طور پر، تینوں Pythagorean ذرائع 4 ہوں گے اگر دی گئی قدریں 4، 4، اور 4 ہیں۔ چونکہ ریاضی کا مطلب عام طور پر استعمال ہوتا ہے، اس لیے ہارمونک وسط اکثر ریاضی کے اوسط سے الجھ جاتا ہے۔ بہت سی جگہوں پر، ہارمونک ذرائع بہترین ممکنہ اوسط دیتے ہیں۔ نوٹ کریں کہ ہارمونک وسط بنیادی طور پر اوسط کے حساب کے لیے استعمال ہوتا ہے جب دی گئی قدر کو تناسب اور شرحوں میں ظاہر کیا جاتا ہے۔

ہم یہ سمجھنے کے لیے ایک اور مثال لینے جا رہے ہیں کہ ریاضی اور ہارمونک ذرائع کا حساب کہاں لگایا جاتا ہے۔

ہارمونک اوسط بمقابلہ ریاضی کا مطلب

مثال کے طور پر گاڑی کی رفتار اور اس کا فاصلہ لیں۔ فرض کریں کہ ایک ٹرین نے ایک خاص رفتار سے سفر کرتے ہوئے ایک مخصوص فاصلہ طے کیا ہے۔ اب، اگر یہ واپسی کے وقت اتنا ہی فاصلہ طے کرتی ہے، تو ہارمونک وسط کا استعمال کرتے ہوئے ٹرین کی اوسط رفتار کا حساب لگایا جائے گا۔ یہ ریاضیاتی فارمولہ آپ کو اوسط رفتار تلاش کرنے میں مدد کرے گا جس سے ٹرین منزل پر واپس آئی ہوگی۔ اگر یہ ٹرین مختلف رفتار سے سفر کرتی ہے اور پھر بھی منزل تک پہنچنے میں مساوی وقت لیتی ہے، تو آپ کو ٹرین کی اوسط رفتار حاصل کرنے کے لیے ریاضی کے اوسط کا حساب لگانے کی ضرورت ہوگی۔

یہی مثال ہر حساب پر لاگو ہوتی ہے، جس میں صارف طے شدہ فاصلے کو دیکھتے ہوئے گاڑی کی اوسط رفتار معلوم کرنے کی کوشش کرتا ہے۔ اگر آپ کی گاڑی ایک ہی فاصلے کو مختلف رفتار سے طے کرتی ہے، تو آپ کو گاڑی کی اوسط رفتار کا حساب لگانے کے لیے ہارمونک مطلب استعمال کرنے کی ضرورت ہے۔