What is the Goodness of Fit Test?

The goodness of fit method is a statistical hypothesis test that determines how well sample data match a normal distribution from a population. To put it another way, this test determines if your sample data is representative of the one that you would anticipate finding in the actual population or whether it is biased in any way.

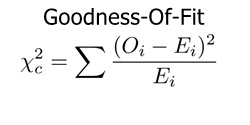
The disparity between the actual values and those anticipated of the model in a normal distribution instance is determined by goodness of fit.

Importance of Goodness of Fit Test

The goodness of fit test is an important test to see if the data observed matches what is predicted. The results of the hypothesis test can be used to make decisions. A shop, for example, needs to know what kinds of products are appealing to young people. To determine which product is favoured, the merchant polls a random sample of old and young individuals.

They use chi-square to determine that there is a link between product A and young people with 90% confidence. Based on these findings, it is possible to conclude that this sample reflects the population of young adults. This may be used by retail marketers to improve their campaigns.

Different Types of Goodness of Fit Test

The goodness of fit can be determined in a variety of ways. The chi-square, the Kolmogorov-Smirnov test, and the Shipiro-Wilk test are some of the most widely used statistical procedures. Let’s learn about these tests in detail.

1. The Chi-Square Test

The chi-square test is an inferential statistics method for evaluating the validity of a population claim based on a random sample. The sort or intensity of the relationship, however, is not indicated. It doesn't say if the connection is good or bad, for example. It works with discrete distributions such as the binomial and Poisson distributions.

Setting the required Alpha level of significance, identifying the categorical variables to test, and defining hypothesis statements regarding the relationships between them are all important steps in calculating the chi-square goodness of fit. The null hypothesis is all about stating that there is no link between variables, while the alternative hypothesis states that there is a link.

2. The Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov test (also called the K-S test) is a statistical procedure that assesses if a sample comes from a given distribution within a population. It is named after Russian mathematicians Andrey Kolmogorov and Nikolai Smirnov. The non-parametric Kolmogorov-Smirnov test, which is suggested for large samples, does not rely on any distribution to be valid. The purpose is to prove the null hypothesis, which is the normal distribution's sample. It can be used only for continuous distributions.

3. The Shipiro-Wilk Test

The Shipiro-Wilk test is used to identify whether or not a sample has a normal distribution. It only evaluates for normality when using a sample with one variable of continuous data. This is best for small sample sizes of up to 2000 people. It employs alpha, much like the others, and creates two hypotheses: null and alternative. The null hypothesis asserts that the sample comes from a normal distribution, whereas the alternative hypothesis states that it does not.

The Bottom Line

The goodness of fit tests examines how well sample data matches what a population should be like. An observed value is derived from the sample data and compared to the predicted expected value using a discrepancy measure. Depending on the conclusion you want, several goodnesses of fit hypothesis tests is available. The best goodness of fit test to use relies heavily on what you want to know about a sample and how big it is.