तंदुरुस्त चाचणीची चांगलीता काय आहे?

तंदुरुस्त पद्धतीची चांगलीता ही एक सांख्यिकीय गृहीतक चाचणी आहे जी नमुना डेटा लोकसंख्येतील सामान्य वितरणाशी किती चांगला जुळतो हे निर्धारित करते. दुसर्‍या मार्गाने सांगायचे तर, ही चाचणी निर्धारित करते की तुमचा नमुना डेटा ज्याचा तुम्हाला वास्तविक लोकसंख्येमध्ये सापडण्याची अपेक्षा आहे किंवा तो कोणत्याही प्रकारे पक्षपाती आहे की नाही याचे प्रतिनिधी आहे.

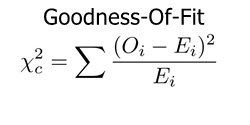
वास्तविक मूल्ये आणि सामान्य वितरण उदाहरणामध्ये अपेक्षित असलेल्या मॉडेलमधील असमानता योग्यतेने निर्धारित केली जाते.

फिट चाचणीच्या चांगुलपणाचे महत्त्व

तंदुरुस्त चाचणीची चांगुलपणा ही एक महत्त्वाची चाचणी आहे की निरीक्षण केलेला डेटा अंदाजानुसार जुळतो की नाही. गृहीतक चाचणीचे परिणाम निर्णय घेण्यासाठी वापरले जाऊ शकतात. एखाद्या दुकानाला, उदाहरणार्थ, तरुणांना कोणत्या प्रकारची उत्पादने आकर्षित करतात हे जाणून घेणे आवश्यक आहे. कोणते उत्पादन पसंतीचे आहे हे निर्धारित करण्यासाठी, व्यापारी वृद्ध आणि तरुण व्यक्तींच्या यादृच्छिक नमुन्याचे सर्वेक्षण करतात.

उत्पादन A आणि 90% आत्मविश्वास असलेल्या तरुण लोकांमध्ये दुवा आहे हे निर्धारित करण्यासाठी ते ची-स्क्वेअर वापरतात. या निष्कर्षांवर आधारित, असा निष्कर्ष काढणे शक्य आहे की हा नमुना तरुण प्रौढांची लोकसंख्या प्रतिबिंबित करतो. हे किरकोळ विक्रेते त्यांच्या मोहिमा सुधारण्यासाठी वापरले जाऊ शकतात.

फिट चाचणीचे विविध प्रकार

तंदुरुस्तीची चांगुलपणा विविध प्रकारे निर्धारित केली जाऊ शकते. ची-स्क्वेअर, कोल्मोगोरोव्ह-स्मिर्नोव्ह चाचणी आणि शिपिरो-विल्क चाचणी या सर्वात मोठ्या प्रमाणावर वापरल्या जाणार्‍या सांख्यिकीय प्रक्रिया आहेत. या चाचण्यांबद्दल सविस्तर जाणून घेऊया.

1. ची-स्क्वेअर चाचणी

यादृच्छिक नमुन्यावर आधारित लोकसंख्येच्या दाव्याच्या वैधतेचे मूल्यमापन करण्यासाठी ची-स्क्वेअर चाचणी ही एक अनुमानित आकडेवारी पद्धत आहे. तथापि, संबंधांची क्रमवारी किंवा तीव्रता दर्शविली जात नाही. उदाहरणार्थ, कनेक्शन चांगले आहे की वाईट हे सांगू शकत नाही. हे द्विपदी आणि पॉसॉन वितरणासारख्या वेगळ्या वितरणासह कार्य करते.

आवश्यक सेट करणेअल्फा महत्त्वाची पातळी, चाचणीसाठी स्पष्ट व्हेरिएबल्स ओळखणे आणि गृहीतके परिभाषित करणेविधाने ची-स्क्वेअर चांगुलपणाची गणना करण्यासाठी त्यांच्यातील संबंधांबद्दल सर्व महत्त्वाचे टप्पे आहेत. शून्य गृहीतक हे असे सांगते की व्हेरिएबल्समध्ये कोणताही दुवा नाही, तर पर्यायी गृहीतक एक दुवा असल्याचे सांगते.

2. कोल्मोगोरोव्ह-स्मिर्नोव्ह चाचणी

कोल्मोगोरोव्ह-स्मिर्नोव्ह चाचणी (याला K-S चाचणी देखील म्हणतात) ही एक सांख्यिकीय प्रक्रिया आहे जी लोकसंख्येतील दिलेल्या वितरणातून नमुना आला आहे का याचे मूल्यांकन करते. हे नाव रशियन गणितज्ञ आंद्रे कोल्मोगोरोव्ह आणि निकोलाई स्मरनोव्ह यांच्या नावावर आहे. नॉन-पॅरामेट्रिक कोल्मोगोरोव्ह-स्मिरनोव्ह चाचणी, जी मोठ्या नमुन्यांसाठी सुचविली जाते, ती वैध होण्यासाठी कोणत्याही वितरणावर अवलंबून नाही. यामागे शून्य गृहीतक सिद्ध करणे हा आहे, जो सामान्य वितरणाचा नमुना आहे. हे केवळ सतत वितरणासाठी वापरले जाऊ शकते.

3. शिपिरो-विल्क चाचणी

शिपिरो-विल्क चाचणीचा वापर नमुनामध्ये सामान्य वितरण आहे की नाही हे ओळखण्यासाठी केला जातो. सतत डेटाच्या एका व्हेरिएबलसह नमुना वापरताना ते केवळ सामान्यतेसाठी मूल्यांकन करते. 2000 लोकांपर्यंत लहान नमुना आकारांसाठी हे सर्वोत्तम आहे. हे अल्फा वापरते, इतरांप्रमाणेच, आणि दोन गृहीतके तयार करते: शून्य आणि पर्यायी. शून्य गृहीतक असे प्रतिपादन करते की नमुना सामान्य वितरणातून येतो, तर पर्यायी गृहीतक असे सांगते की तसे होत नाही.

तळ ओळ

तंदुरुस्त चाचण्यांचे चांगुलपणा हे तपासते की नमुना डेटा लोकसंख्या कशी असावी याशी किती जुळते. निरीक्षण केलेले मूल्य नमुना डेटामधून घेतले जाते आणि विसंगती माप वापरून अंदाजित अपेक्षित मूल्याशी तुलना केली जाते. तुम्हाला हव्या असलेल्या निष्कर्षावर अवलंबून, तंदुरुस्त गृहीतक चाचण्यांच्या अनेक चांगुलपणा उपलब्ध आहेत. तंदुरुस्त चाचणीचा वापर करण्यासाठी सर्वोत्तम चांगुलपणा तुम्हाला नमुन्याबद्दल काय जाणून घ्यायचे आहे आणि ते किती मोठे आहे यावर खूप अवलंबून असते.