Table of Contents

பெரிய எண்களின் சட்டம்

Updated on October 3, 2024 , 7154 views

பெரிய எண்களின் சட்டம் என்றால் என்ன?

நிதிக் கண்ணோட்டத்தில், பெரிய எண்களின் சட்டம், விரைவான வளர்ச்சி மற்றும் வளர்ச்சியை அனுபவித்து வரும் ஒரு பெரிய நிறுவனம் விண்வெளி வேகத்தில் எப்போதும் வளர முடியாது என்று கூறுகிறது. இது பெரும்பாலும் சதவீதங்களில் கணக்கிடப்படுகிறது. வணிகத்தின் வளர்ச்சி வேகம் எப்போதும் ஒரே மாதிரியாக இருக்க வாய்ப்பில்லை என்று அது கூறுகிறது. பெரிய எண்களின் தோற்றம் பற்றிய சட்டம் 16 ஆம் நூற்றாண்டில் தோன்றியது. "ஜெரோலாமா கார்டானோ" என்ற புகழ்பெற்ற கணிதவியலாளர் சட்டத்தை அடையாளம் காட்டினார். எனினும் அவரால் நிரூபிக்க முடியவில்லை. இறுதியில், ஜேக்கப் பெர்னோலி இந்த சட்டத்தை 1713 இல் நிரூபித்தார்.

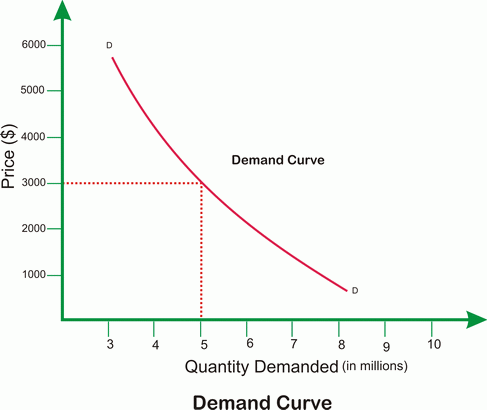
பெரிய எண்களின் சட்டம் பொதுவாக புள்ளிவிவரங்களில் பயன்படுத்தப்படுகிறது. உண்மையில், சட்டம் வெவ்வேறு பாடங்களுக்கு பொருந்தும். கொடுக்கப்பட்ட மக்கள்தொகையிலிருந்து ஒவ்வொரு நபருக்கும் தேவையான தரவுகளைச் சேகரிப்பது நடைமுறையில் சாத்தியமில்லை. எவ்வாறாயினும், நீங்கள் அதிகமான நபர்களை கணக்கெடுப்பதால், நீங்கள் பெறும் முடிவு துல்லியமானதாகவோ அல்லது சராசரிக்கு நெருக்கமாகவோ இருக்கும் வாய்ப்புகள் அதிகம். வணிகம் மற்றும் புள்ளிவிவரங்களின் அடிப்படையில் பெரிய எண்களின் சட்டத்தின் பயன்பாட்டைப் புரிந்துகொள்வோம்.

பெரிய எண்கள் மற்றும் வணிக வளர்ச்சிக்கான சட்டம்

வணிக மற்றும் நிதித் துறையில், பெரிய எண்களின் சட்டம் நிறுவனத்தின் வளர்ச்சி சுழற்சியைக் குறிக்கிறது. மேலே குறிப்பிட்டுள்ளபடி, நிறுவனம் எல்லா நேரத்திலும் ஒரே விகிதத்தில் வளர முடியாது என்று அது அறிவுறுத்துகிறது. இருப்பினும், இந்த கவனிப்பு பெரிய எண்களின் சட்டத்திலிருந்து இல்லை. இது குறுகலான வருமானத்தை குறைக்கும் சட்டத்திலிருந்து பெறப்பட்டது.

உதாரணமாக, Walmart Inc. 2015 ஆம் ஆண்டில் $485.5 பில்லியன் வருவாய் ஈட்டியுள்ளது. அதே ஆண்டில், Amazon 95.8 பில்லியன் டாலர் வருவாய் ஈட்டியுள்ளது. Walmart Inc அதன் வளர முடிவு செய்தால்வருமானம் 50%, அது கூடுதலாக $242 பில்லியன் ஈட்ட வேண்டியிருந்தது. மறுபுறம், அதே இலக்கை அடைய Amazon க்கு $47.9 பில்லியன் மட்டுமே தேவைப்படும். இப்போது, அமேசானை விட வால்மார்ட் தனது வருவாயை 50% அதிகரிப்பது மிகவும் சவாலானதாக இருக்கும் என்று பெரிய எண்களின் சட்டம் தெரிவிக்கிறது.

Ready to Invest?
Talk to our investment specialist

புள்ளிவிபரத்தில் பெரிய எண்களின் சட்டம்

புள்ளிவிவரங்களில், பெரிய எண்களின் விதியை ஒரு தேற்றம் என வரையறுக்கலாம், இது ஒரு பரிசோதனையை பல முறை செய்வதன் முடிவைக் கூறுகிறது. அதிக எண்ணிக்கையிலான சோதனைகளில் இருந்து உருவாக்கப்படும் முடிவு எதிர்பார்க்கப்படும் மதிப்பிற்கு அருகில் இருக்கும் என்று சட்டம் பரிந்துரைக்கிறது. அதுமட்டுமின்றி, அதிக பரிசோதனைகள் செய்யப்படுவதால், சராசரியை நெருங்க வாய்ப்புள்ளது. தேற்றம் ஒரு நிலையான நீண்ட கால முடிவை வழங்குவதால் புள்ளிவிவரங்களில் மிகவும் முக்கியமானது.

இதை ஒரு உதாரணத்தின் மூலம் புரிந்து கொள்வோம். நீங்கள் ஒரு சூதாட்ட விடுதியில் ரவுலட் சக்கரத்தை சுழற்றுகிறீர்கள் என்று வைத்துக்கொள்வோம். நீங்கள் சுற்றில் வெற்றி பெறுவீர்கள். கேசினோ ஒரு ஸ்பின் இழந்திருக்க வேண்டும், ஆனால் நீங்கள் அதிக எண்ணிக்கையிலான சுழல்களை செய்தால், முடிவுகள் கேசினோவிற்கு சாதகமாக இருக்கும். வேறு வார்த்தைகளில் கூறுவதானால், ஒவ்வொரு சுழற்சியிலும் கேசினோ அதன் எதிர்பார்க்கப்படும் அல்லது கணிக்கக்கூடிய மதிப்பை நெருங்குவதற்கு ஒரு நல்ல வாய்ப்பு உள்ளது.

இங்கு கவனிக்க வேண்டிய ஒரு முக்கியமான விஷயம் என்னவென்றால், அதிக எண்ணிக்கையிலான சோதனைகள் அல்லது பரிசோதனைகள் செய்யப்படும் முடிவுகளுக்கு பெரிய எண்களின் சட்டம் பொருந்தும்.

Disclaimer:
இங்கு வழங்கப்பட்ட தகவல்கள் துல்லியமானவை என்பதை உறுதிப்படுத்த அனைத்து முயற்சிகளும் மேற்கொள்ளப்பட்டுள்ளன. இருப்பினும், தரவின் சரியான தன்மை குறித்து எந்த உத்தரவாதமும் அளிக்கப்படவில்லை. முதலீடு செய்வதற்கு முன் திட்டத் தகவல் ஆவணத்துடன் சரிபார்க்கவும்.