Table of Contents
- Understanding the Fibonacci Sequence
- Formula for the Fibonacci Sequence
- Fibonacci Sequence List
- Fibonacci Sequence Example
- The Intriguing Origin of Fibonacci Sequence
- Nature's Numerical Signature
- The Golden Ratio
- Fibonacci in Financial Markets
- Applying Fibonacci in Technical Analysis
- How Does the Fibonacci Sequence Influence Trading Behaviour?
- The Psychology of Fibonacci Levels
- Fibonacci in Art and Architecture
- Beyond Fibonacci: Fractals and Chaos Theory
- Conclusion
What is the Fibonacci Sequence and How it Works?
The Fibonacci sequence, a captivating numerical phenomenon, has intrigued mathematicians, scientists, and enthusiasts for centuries. Named after the Italian mathematician Leonardo Fibonacci, who introduced it to the Western world, this sequence boasts a mesmerising pattern deeply rooted in nature, art, and financial markets.
The Fibonacci sequence constitutes a numerical series where every number is the sum of the two preceding ones, typically commencing with 0 and 1. In mathematics, a sequence denotes an ordered collection of numbers adhering to a specific pattern, where the individual numbers are referred to as terms. This article helps you explore the definition, formula, list, and examples associated with the Fibonacci sequence.
Understanding the Fibonacci Sequence
At its core, the Fibonacci sequence is a series of numbers where every number is the total of the two preceding ones. It begins with 0 and 1, resulting in the arrangement 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. Mathematically expressed, each term (Fibonacci number) is obtained by adding the two preceding terms: F(n) = F(n-1) + F(n-2).
Formula for the Fibonacci Sequence
The formula defining the Fibonacci sequence of numbers, denoted as "Fn," employs a recursive relation with initial values set as F0=0 and F1=1:
Fn = Fn-1 + Fn-2
This formulation comprises two distinct components: the kick-off phase and the recursive relation.
The kick-off phase establishes the seed values as F0=0 and F1=1.
The recursive relation component, expressed as Fn = Fn-1 + Fn-2, dictates the generation of subsequent terms based on the preceding two. Notably, the sequence commences with 0, making F5 represent the 6th term in the sequence.
Check Here!
Fibonacci Sequence List
List of the first 20 terms in the Fibonacci Sequence:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181
The Fibonacci numbers list is calculated as follows:
| Fn | Fibonacci Number |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| So on… | So on… |
Fibonacci Sequence Example
Let's understand this further with an example. Using the recursive relation, we must determine the Fibonacci number when n = 5.
The solution to this would be as follows:
The formula for calculating the Fibonacci Sequence is given by:
Fn = Fn-1 + Fn-2
Consider: F0 = 0 and F1 = 1 Applying the formula, we get
- F2 = F1 + F0 = 1 + 0 = 1
- F3 = F2 + F1 = 1 + 1 = 2
- F4 = F3 + F2 = 2 + 1 = 3
- F5 = F4 + F3 = 3 + 2 = 5
Therefore, the Fibonacci number when n = 5 is 5.
The Intriguing Origin of Fibonacci Sequence
While commonly associated with Leonardo Fibonacci, the sequence's roots trace back to ancient Indian mathematics. Indian mathematician Acarya Virahanka, around 600 A.D., is credited with developing Fibonacci numbers and the sequence method. This sequence was then referenced and expanded upon by subsequent Indian mathematicians like Gopala, Hemacandra, and Narayana Pandita.
Nature's Numerical Signature
The Fibonacci sequence's enchantment lies in its pervasive presence in the natural world. It manifests in the arrangement of leaves, petals, and seeds in plants, the spirals of shells, and the reproductive patterns of rabbits. The mesmerising spiral patterns in seashells and galaxies often adhere to Fibonacci proportions, showcasing the sequence's imprint on the universe's design.
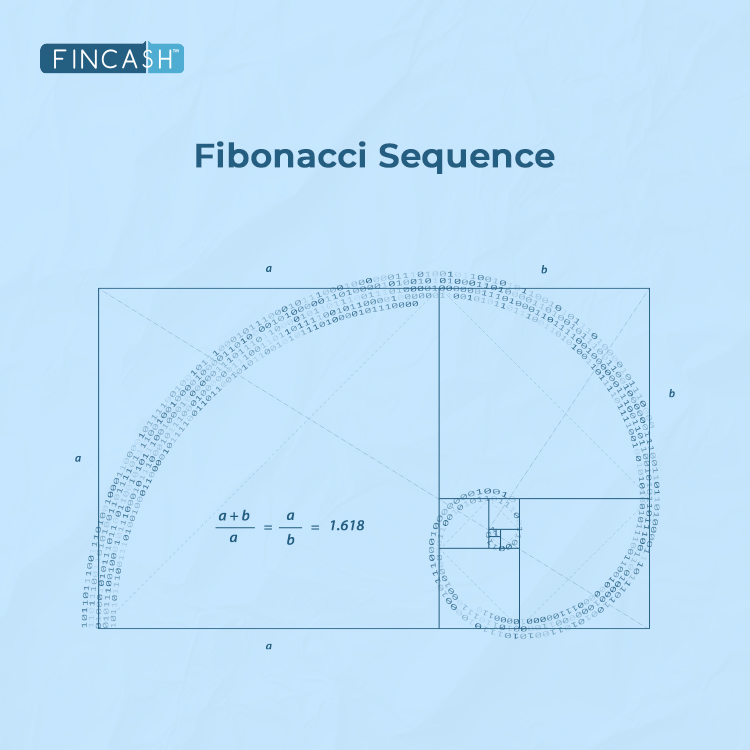
The Golden Ratio
The Fibonacci sequence is intimately connected to the golden ratio, which is an irrational number roughly equal to 1.618. The golden ratio is a unique mathematical constant that appears when ratios of Fibonacci numbers converge. This ratio, denoted by the Greek letter phi (φ), possesses aesthetic significance and is prevalent in art, architecture, and design.
For instance, consider the pair of Fibonacci numbers 3 and 5; the ratio of 5 to 3 is:
- 5/3 = 1.666635 = 1.6666
Taking another pair, such as 21 and 34, the ratio of 34 to 21 is:
- 34/21 = 1.6192134 = 1.619
This observation indicates that as the Fibonacci numbers in a pair increase in value, their ratio approaches the Golden Ratio.
The formula to calculate Fibonacci numbers utilising the Golden Ratio is expressed as:
Xn = ϕn−(1−ϕ)n/√5
Here, ϕ represents the Golden Ratio, approximately 1.618, and n represents the term number in the sequence.
Fibonacci in Financial Markets
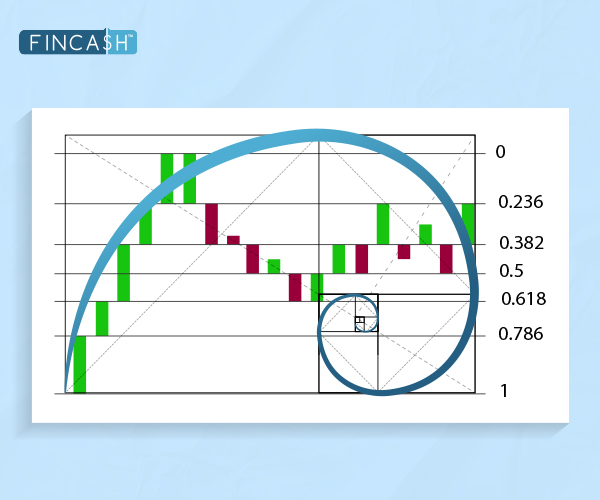
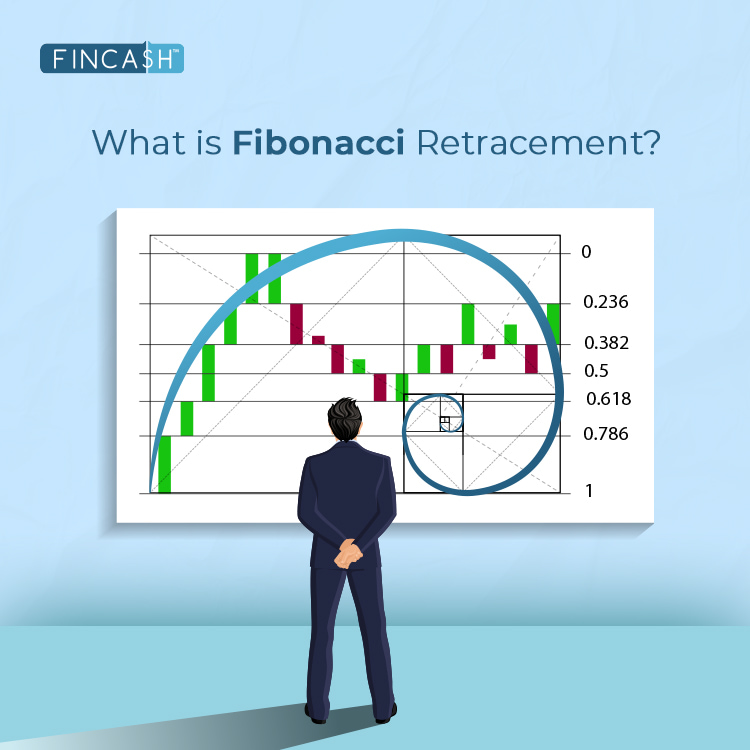
Beyond nature and art, the Fibonacci sequence is fascinating in financial markets. Traders and analysts use Fibonacci Retracements, a Technical Analysis tool, to classify potential support and resistance levels. These retracement levels are derived from the Fibonacci sequence and are applied to price charts to predict potential reversals or pauses in a Financial Instrument's trend.
Applying Fibonacci in Technical Analysis
Fibonacci retracement levels, commonly set at 23.6%, 38.2%, 50%, 61.8%, and 78.6%, are plotted on a price chart between a high and a low. These levels help traders identify key areas where an asset might reverse or experience a significant pullback. The concept is that these levels represent potential support or resistance zones based on the historical relationship between the Fibonacci numbers.
How Does the Fibonacci Sequence Influence Trading Behaviour?
Humans naturally recognise patterns, and traders often associate patterns in charts with the Fibonacci sequence. While the direct correlation of Fibonacci numbers to fundamental Market forces remains unproven, markets inherently respond to the beliefs and actions of participants. Therefore, when investors make buying or selling decisions based on Fibonacci analysis, they contribute to a self-fulfilling prophecy that can influence market trends.
The Psychology of Fibonacci Levels
The efficacy of Fibonacci retracements is often attributed to the psychological behaviour of traders. As many market participants know these levels, it creates a self-fulfilling prophecy. Traders might place buy or sell orders at these levels, amplifying their significance in Market Dynamics.
Fibonacci in Art and Architecture
The allure of the Fibonacci sequence extends into art and architecture. Renowned artists and architects, knowingly or unknowingly, have incorporated Fibonacci proportions into their creations. The Parthenon in Athens and the spirals of the nautilus shell are notable examples where the sequence's mathematical elegance converges with artistic expression.
Beyond Fibonacci: Fractals and Chaos Theory
The influence of the Fibonacci sequence expands into fractals and chaos theory. Fractals, intricate and self-replicating geometric patterns, often exhibit Fibonacci sequences within their structures. This connection underscores the deep interplay between mathematics and the complexities of nature.
Conclusion
With its ancient origins and far-reaching influence, the Fibonacci sequence weaves an intricate tapestry across disciplines. From the natural world's patterns to the financial markets rhythms, this numerical marvel captivates minds and underscores the profound interconnectedness of mathematics with the fabric of our universe. The enduring legacy of the Fibonacci sequence lies not just in its mathematical elegance but in its ability to reveal the beauty and harmony that permeate the diverse landscapes of science, nature, and human creativity.
All efforts have been made to ensure the information provided here is accurate. However, no guarantees are made regarding correctness of data. Please verify with scheme information document before making any investment.
You Might Also Like