फिट टेस्ट की अच्छाई क्या है?

फिट विधि की अच्छाई एक सांख्यिकीय परिकल्पना परीक्षण है जो यह निर्धारित करती है कि नमूना डेटा जनसंख्या से सामान्य वितरण से कितनी अच्छी तरह मेल खाता है। दूसरे शब्दों में, यह परीक्षण यह निर्धारित करता है कि क्या आपका नमूना डेटा उस डेटा का प्रतिनिधि है जिसे आप वास्तविक जनसंख्या में खोजने की उम्मीद करेंगे या यह किसी भी तरह से पक्षपाती है या नहीं।

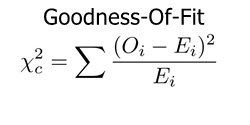
एक सामान्य वितरण उदाहरण में वास्तविक मूल्यों और मॉडल के प्रत्याशित मूल्यों के बीच असमानता फिट की अच्छाई से निर्धारित होती है।

फिट टेस्ट की अच्छाई का महत्व

फिट टेस्ट की अच्छाई यह देखने के लिए एक महत्वपूर्ण परीक्षण है कि क्या देखा गया डेटा भविष्यवाणी से मेल खाता है। परिकल्पना परीक्षण के परिणामों का उपयोग निर्णय लेने के लिए किया जा सकता है। उदाहरण के लिए, एक दुकान को यह जानने की जरूरत है कि किस तरह के उत्पाद युवा लोगों को आकर्षित कर रहे हैं। यह निर्धारित करने के लिए कि कौन सा उत्पाद पसंदीदा है, व्यापारी बूढ़े और युवा व्यक्तियों के यादृच्छिक नमूने का चुनाव करता है।

वे ची-स्क्वायर का उपयोग यह निर्धारित करने के लिए करते हैं कि उत्पाद ए और 90% आत्मविश्वास वाले युवाओं के बीच एक कड़ी है। इन निष्कर्षों के आधार पर यह निष्कर्ष निकालना संभव है कि यह नमूना युवा वयस्कों की जनसंख्या को दर्शाता है। इसका उपयोग खुदरा विपणक अपने अभियानों को बेहतर बनाने के लिए कर सकते हैं।

फिट टेस्ट की विभिन्न प्रकार की अच्छाई

फिट की अच्छाई को विभिन्न तरीकों से निर्धारित किया जा सकता है। ची-स्क्वायर, कोलमोगोरोव-स्मिरनोव परीक्षण और शिपिरो-विल्क परीक्षण कुछ सबसे व्यापक रूप से उपयोग की जाने वाली सांख्यिकीय प्रक्रियाएं हैं। आइए इन परीक्षणों के बारे में विस्तार से जानें।

1. ची-स्क्वायर टेस्ट

ची-स्क्वायर परीक्षण एक यादृच्छिक नमूने के आधार पर जनसंख्या के दावे की वैधता का मूल्यांकन करने के लिए एक अनुमानित सांख्यिकी पद्धति है। हालाँकि, रिश्ते के प्रकार या तीव्रता का संकेत नहीं दिया गया है। उदाहरण के लिए, यह नहीं बताता कि कनेक्शन अच्छा है या बुरा। यह द्विपद और पॉइसन वितरण जैसे असतत वितरण के साथ काम करता है।

आवश्यक सेटिंगअल्फा महत्व का स्तर, परीक्षण के लिए श्रेणीबद्ध चर की पहचान करना और परिकल्पना को परिभाषित करनाबयान उनके बीच संबंधों के संबंध में फिट की ची-स्क्वायर अच्छाई की गणना में सभी महत्वपूर्ण कदम हैं। शून्य परिकल्पना यह बताने के बारे में है कि चर के बीच कोई संबंध नहीं है, जबकि वैकल्पिक परिकल्पना बताती है कि एक लिंक है।

2. कोलमोगोरोव-स्मिरनोव टेस्ट

कोलमोगोरोव-स्मिरनोव परीक्षण (जिसे के-एस परीक्षण भी कहा जाता है) एक सांख्यिकीय प्रक्रिया है जो यह आकलन करती है कि क्या नमूना आबादी के भीतर दिए गए वितरण से आता है। इसका नाम रूसी गणितज्ञ एंड्री कोलमोगोरोव और निकोलाई स्मिरनोव के नाम पर रखा गया है। गैर-पैरामीट्रिक कोलमोगोरोव-स्मिरनोव परीक्षण, जो बड़े नमूनों के लिए सुझाया गया है, मान्य होने के लिए किसी भी वितरण पर निर्भर नहीं करता है। इसका उद्देश्य शून्य परिकल्पना को सिद्ध करना है, जो सामान्य वितरण का नमूना है। इसका उपयोग केवल निरंतर वितरण के लिए किया जा सकता है।

3. शिपिरो-विल्क टेस्ट

शिपिरो-विल्क परीक्षण का उपयोग यह पहचानने के लिए किया जाता है कि किसी नमूने का वितरण सामान्य है या नहीं। निरंतर डेटा के एक चर के साथ नमूने का उपयोग करते समय यह केवल सामान्यता के लिए मूल्यांकन करता है। यह 2000 लोगों तक के छोटे नमूने के आकार के लिए सबसे अच्छा है। यह अल्फा का उपयोग करता है, बहुत कुछ दूसरों की तरह, और दो परिकल्पनाएँ बनाता है: अशक्त और वैकल्पिक। शून्य परिकल्पना का दावा है कि नमूना सामान्य वितरण से आता है, जबकि वैकल्पिक परिकल्पना में कहा गया है कि ऐसा नहीं है।

तल - रेखा

फिट परीक्षणों की अच्छाई इस बात की जांच करती है कि नमूना डेटा कितनी अच्छी तरह मेल खाता है कि जनसंख्या कैसी होनी चाहिए। एक प्रेक्षित मान नमूना डेटा से प्राप्त किया जाता है और एक विसंगति माप का उपयोग करके अनुमानित अपेक्षित मूल्य की तुलना में किया जाता है। आप जो निष्कर्ष चाहते हैं उसके आधार पर, फिट परिकल्पना परीक्षणों की कई अच्छाईयां उपलब्ध हैं। उपयोग करने के लिए फिट परीक्षण की सबसे अच्छी अच्छाई इस बात पर बहुत अधिक निर्भर करती है कि आप किसी नमूने के बारे में क्या जानना चाहते हैं और यह कितना बड़ा है।