अनुकूल माध्य

हार्मोनिक माध्य क्या है?

दिए गए आंकड़ों के हार्मोनिक माध्य की गणना करने के लिए, आपको प्रत्येक संख्या के पारस्परिक द्वारा अवलोकनों की कुल संख्या को विभाजित करना चाहिए। आइए एक उदाहरण के साथ हार्मोनिक माध्य परिभाषा को समझते हैं।

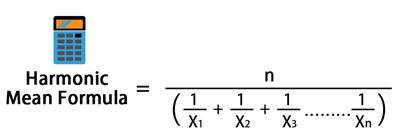
मान लीजिए आपको 1, 3, 5, और 10 के हार्मोनिक माध्य की गणना करने के लिए कहा जाता है। अब जब आपके पास कुल 4 अवलोकन हैं, तो आप 4 को प्रत्येक संख्या के पारस्परिक योग से विभाजित करेंगे, अर्थात 1/1 + 1/3 + 1/5 + 1/10। इन व्युत्क्रमों के योग से प्राप्त कुल योग को 4 से विभाजित करने पर, आपको इस गणना का हार्मोनिक माध्य प्राप्त होगा।

हार्मोनिक माध्य का अवलोकन

उप-विपरीत माध्य के रूप में भी जाना जाता है, हार्मोनिक माध्य को दिए गए आंकड़ों के औसत की गणना के लिए एक सामान्य गणना विकल्प के रूप में माना जाता है। यह ध्यान रखना महत्वपूर्ण है कि हार्मोनिक माध्य अवतल होता है। कहा जा रहा है कि, आपको उन संख्याओं पर विशेष ध्यान देने की आवश्यकता है जिनका उपयोग आप औसत की गणना के लिए करते हैं। यहां, आप ऋणात्मक संख्याओं का उपयोग नहीं कर सकते हैं।

हार्मोनिक माध्य पाइथागोरस माध्य का एक भाग है, जिसमें कुल तीन साधन होते हैं (पहला और दूसरा क्रमशः अंकगणितीय माध्य और ज्यामितीय माध्य होता है)। यदि दिए गए मान समान हैं तो हार्मोनिक माध्य अंकगणितीय और ज्यामितीय माध्य के समान होगा।

उदाहरण के लिए, सभी तीन पाइथागोरस माध्य 4 होंगे यदि दिए गए मान 4, 4, और 4 हैं। चूंकि अंकगणितीय माध्य काफी सामान्य रूप से उपयोग किया जाता है, इसलिए हार्मोनिक माध्य अक्सर अंकगणितीय माध्य के साथ भ्रमित होता है। कई जगहों पर, हार्मोनिक साधन सर्वोत्तम संभव औसत देते हैं। ध्यान दें कि हार्मोनिक माध्य मुख्य रूप से औसत की गणना के लिए उपयोग किया जाता है जब दिए गए मान को अनुपात और दरों में व्यक्त किया जाता है।

हम यह समझने के लिए एक और उदाहरण लेने जा रहे हैं कि अंकगणित और हार्मोनिक साधनों की गणना कहाँ की जाती है।

हार्मोनिक माध्य बनाम अंकगणित माध्य

उदाहरण के लिए, वाहन की गति और उसकी दूरी को लें। मान लीजिए कि एक ट्रेन ने एक विशेष गति से यात्रा करते हुए एक विशिष्ट दूरी तय की है। अब, यदि यह लौटते समय समान दूरी तय करती है, तो ट्रेन की औसत गति की गणना हार्मोनिक माध्य का उपयोग करके की जाएगी। यह गणितीय सूत्र आपको उस औसत गति का पता लगाने में मदद करेगा जिस पर ट्रेन अपने गंतव्य पर वापस आई होगी। यदि यह ट्रेन अलग-अलग गति से यात्रा करती है, फिर भी गंतव्य तक पहुंचने में समान समय लेती है, तो आपको ट्रेन की औसत गति प्राप्त करने के लिए अंकगणितीय माध्य की गणना करने की आवश्यकता होगी।

यही उदाहरण हर गणना पर लागू होता है, जिसमें उपयोगकर्ता तय की गई दूरी को देखते हुए वाहन की औसत गति का पता लगाने की कोशिश करता है। यदि आपका वाहन अलग-अलग गति से समान दूरी तय करता है, तो आपको वाहन की औसत गति की गणना करने के लिए हार्मोनिक माध्य का उपयोग करने की आवश्यकता है।