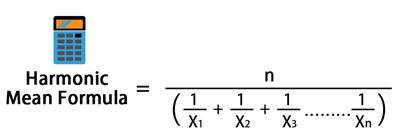अंकगणित माध्य क्या है?

अंकगणित माध्य औसत के आमतौर पर इस्तेमाल किए जाने वाले और सार्वभौमिक रूप से स्वीकृत माप को संदर्भित करता है। आमतौर पर गणित में उपयोग किया जाता है, अंकगणितीय माध्य का व्यापक होता हैश्रेणी आवेदनों की। अंकगणितीय माध्य में, दी गई संख्याओं के समूह के योग की गणना की जाती है और योग को कुल संख्याओं की गणना से विभाजित किया जाता है।

अंकगणित माध्य सूत्र

x¯=1n∑ni=1xi

x¯ xi मानों के समग्र माध्य को दर्शाता है।

यह परिणाम देता है;

nx¯=∑i=1nxi

इसका मतलब है कि अंकगणितीय माध्य x¯ में मूल डेटा के समान योग देने वाली संख्या की 'n' प्रतियां हैं।

यदि डेटा को xi के लिए i = 1, 2, 3, ….., n के साथ fi घटनाओं के साथ समूहीकृत किया जाता है; तब माध्य को इस प्रकार दर्शाया जाता है:

x¯=∑ni=1fixi∑ni=1fi,

उदाहरण के लिए, नीचे सूचीबद्ध संख्याओं के अंकगणितीय माध्य की गणना निम्नानुसार की जाएगी:

1, 5, 8, 10, 11

एएम = 1 + 5 + 8 + 10 + 11/5

35

गणितीय गणना के लिए व्यापक रूप से उपयोग किए जाने वाले माध्य के दो सबसे सामान्य प्रकार हैं ज्यामितीय माध्य औरअनुकूल माध्य. ये शब्द ज्यादातर निवेश और वित्तीय उद्योग में उपयोग किए जाते हैं। छंटनी का मतलब भी इन दिनों काफी आम है। यह विशेष रूप से उपभोक्ता मूल्य सूचकांक के साथ-साथ व्यक्तिगत उपभोग व्यय की गणना के लिए उपयोग किया जाता है।

अंकगणित माध्य का उपयोग वित्त में भी किया जाता है। मान लीजिए आप जानना चाहते हैंआय आपके उद्योग में 10 शोधकर्ताओं का अनुमान। आपको बस इतना करना है कि सभी 10 शोधकर्ताओं की आय का योग प्राप्त करें और इसे 10 से विभाजित करें। यह आपको अंकगणितीय माध्य देगा। अंकगणित माध्य की गणना काफी सरल और सीधी है। गणित और वित्त का बुनियादी ज्ञान रखने वाले भी अंकगणितीय माध्य को सरल चरणों में माप सकते हैं। जब आपके पास गणना करने के लिए संख्याओं का एक बड़ा समूह होता है तब भी माध्य आपको प्रभावी परिणाम प्रदान करता है।

अंकगणित माध्य की कमियां

अंकगणितीय माध्य सबसे अच्छा विकल्प नहीं है, खासकर जब एक बाहरी व्यक्ति में काफी हद तक माध्य को बदलने की क्षमता होती है। मान लीजिए आप जानना चाहते हैं कि एक विशिष्ट स्कूल के प्रत्येक छात्र को कितना भत्ता मिलता है। इनमें से 9 छात्रों को हर हफ्ते 600 रुपये से लेकर 800 रुपये तक का भत्ता मिलता है। मान लें कि अंतिम बच्चे को INR 1000 का भत्ता मिलता है। यहाँ, अंकगणितीय माध्य औसत का उचित अनुमान नहीं देगा।

ऐसी स्थिति में, आपको माध्यिका की गणना करके एक सटीक अनुमान प्राप्त करने में सक्षम होना चाहिए। इसी तरह, अंकगणित माध्य उन लोगों के लिए सबसे अच्छा विकल्प नहीं है जो किसी के प्रदर्शन का पता लगाना चाहते हैंइन्वेस्टर. अंकगणितीय माध्य सबसे अच्छा और सटीक अनुमान उत्पन्न नहीं करेगा यदिचक्रवृद्धि ब्याज स्थिति में शामिल है। जबकि अंकगणित माध्य का उपयोग वित्त और निवेश उद्योगों में किया जा सकता है, यह वर्तमान और भविष्य के नकदी प्रवाह की गणना के लिए एक आदर्श विकल्प नहीं बनाता है। शोधकर्ताओं और विश्लेषकों को लेना चाहिएनकदी प्रवाह के लिए फर्म के लाभ और हानि का पता लगाते समय विचार मेंवित्तीय वर्ष.

यदि संगठन के नकदी प्रवाह की गणना अंकगणितीय माध्य पद्धति का उपयोग करके की जाती है, तो यह गलत आंकड़े देगा। निवेश पोर्टफोलियो और ऐसी अन्य निवेश संबंधी आवश्यकताओं के लिए, ज्यामितीय माध्य का उपयोग उचित गणना के लिए किया जाता है। ज्यादातर, वित्तीय उद्योग में निवेश से उत्पन्न रिटर्न सहसंबद्ध होते हैं। समीकरण में जितनी अधिक संख्याएँ शामिल होंगी, सूत्र उतना ही पेचीदा होगा। और, माध्य की गणना करना सुपर चुनौतीपूर्ण हो जाएगा।