Table of Contents
Black Scholes Model
The Black-Scholes model is one of the most basic principles in modern financial theory. Fischer Black, Robert Merton, and Myron Scholes developed it in 1973, and it is still commonly used today. It is commonly regarded as one of the most effective methods for calculating the Fair Value of options.
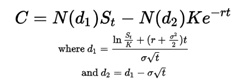
It was the first commonly used model for option pricing, also known as Black-Scholes-Merton (BSM). Present equity values, expected dividends, the option's strike price, expected interest rates, time to expiration, and expected Volatility are 5 input variables used to calculate the theoretical value of options by the Black Scholes model. In Economics, the Black-Scholes model was awarded the Nobel Prize.
Definition of Black Scholes Model
The Black–Scholes / Black–Scholes–Merton model is a statistical model for the dynamics of a stock Market involving derivative investment instruments. It's used to calculate the fair price or potential value of a Call or Put Option based on six factors: leverage, option type, Underlying stock price, time, strike price, and risk-free cost. The model, in particular, predicts how financial instruments can fluctuate over time. The standard BSM model is merely accustomed to European market options.
The Formula of the Black Scholes Model
Black- Scholes Call Option formula is calculated by multiplying the stock price and cumulative standard normal probability distribution function. The strike price's Net present value (NPV) is multiplied by the cumulative standard normal distribution, and then it is subtracted from the previous calculation's result.
In mathematical notation, the formula will be as follow:
C = SN (d1) - Ke^-rt N(d2) Where, C = Price of a call option S = Price of current stock N = A normal distribution K = Strike price R = Risk- free rate of interest T = Maturity time period O = volatility of returns of the Underlying Asset D1 = {1n (S/K) + (R+ O^2/2) T} / √T D2 = D1 - O √T
Talk to our investment specialist
Assumptions about Black Scholes Model
The original Black-Scholes model assumes that the market contains a minimum of one volatile asset like a stock and one essentially risk-free asset like a market fund, cash, or government bond.
Assumptions about the assets within the market are:
- The risk-free asset's rate of return is presumed to be constant.
- The risky asset's price is assumed to function as constant drift and uncertainty, more generally, according to Geometric Brownian Motion.
- There is no dividend paid on the volatile asset.
Assumptions about the market itself are:
- There are no arbitrage (risk-free profit) opportunities.
- Any sum of Capital can be borrowed and lent at the same rate as the risk-free asset's interest rate.
- Any amount of stock can be bought and sold (including short selling).
- Purchasing the option has no processing costs, which means there is no commission for buying or selling securities or derivative instruments.
Limitations of Black Scholes Model
- Dividends and risk-free yields are assumed to be stable in the model, but this may not be the case in practice.
- The model also assumes that volatility is constant over the option's life, which is incorrect since volatility varies with supply and demand.
All efforts have been made to ensure the information provided here is accurate. However, no guarantees are made regarding correctness of data. Please verify with scheme information document before making any investment.