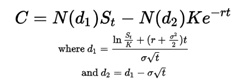Table of Contents
What is a Gordon Growth Model?
The Gordon Growth Model (GGM) is helpful to calculate a stock's Intrinsic Value based on a sequence of dividends that rise at a consistent pace in the future. It's a common and basic dividend discount Model Option (DDM). It solves the present value of an endless series of future payouts, assuming that dividends grow at a constant rate in perpetuity.
Because the model implies a steady growth rate, it is often only applied to corporations with consistent dividend per share growth rates.
Briefly Understanding the Gordon Growth Model
The Gordon Growth Model evaluates a company's stock based on the premise that payments to common equity shareholders will grow at a constant rate. Dividends Per Share (DPS), dividend growth rate, and needed Rate of Return (RoR) are the three main inputs in the model.
The GGM seeks to compute a stock's Fair Value regardless of Market conditions, taking into account dividend payout components and market expected returns. If the model's value is more than the current trading price of shares, the stock is deemed cheap and should be purchased, and vice versa.
Dividends per share are the annual payments a firm provides to its common equity owners, and the dividend growth rate is the percentage increase in dividends per share from one year to the next. The necessary rate of return is the minimal rate of return that investors are willing to accept when purchasing a company's shares. It is calculated using various techniques.
GGM assumes a corporation will operate in perpetuity and will pay steady dividends per share. The model took an infinite series of dividends per share and discounted them back into the present using the needed rate of return to determine the value of a stock.
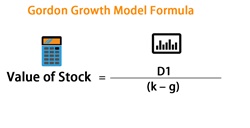
The formula is based on the mathematical principles of an endless series of rising numbers.
P= (D1) / (r-g)
Here,
- P = Present stock price
- g = Present rate of growth expected for dividends
- r = Company’s constant equity Capital cost
- D1 = Next year’s value of the dividend
The Gordon growth model's fundamental flaw is that it assumes that dividends per share would grow at a constant rate. Because of the economic cycles and unanticipated financial troubles or achievements, it is scarce for corporations to show consistent dividend growth. As a result, the approach is limited to companies with constant growth rates.
The relationship between the utilized growth rate and the discount Factor in the model is the second issue. The outcome is a negative value, rendering the model useless if the needed return rate is lower than the dividends per share growth rate. The value per share approaches infinity if the required rate of return is the same as the growth rate.
Talk to our investment specialist
Example of Gordon Growth Model
Consider the case of a corporation whose stock is now trading at 110 USD per share. This corporation needs an 8% minimum rate of return (r) and will pay a 3 USD dividend per share (D1) next year, which is predicted to grow by 5% annually (g).
P = 3 / (0.8 - 0.5) = 100 USD
The shares are currently 10 USD overvalued in the market, according to the Gordon Growth Model.
Gordon Growth Model Assumption
The GGM seeks to determine a stock's fair value regardless of market conditions, taking into account dividend distribution considerations as well as market expected returns. If the GGM value is more than the stock's current market price, the stock is undervalued and should be purchased. In contrast, if the value is less than the current market price, the stock is considered overvalued and should be sold.
What are the Gordon Growth Model's Inputs?
The DPS, the required return rate, and the growth rate in dividends per share are the three essential inputs in GGM. The DPS growth rate is the annual increase in dividends paid by a firm to its common equity shareholders. In contrast, the DPS is the yearly payments made to its common equity shareholders. When purchasing a company's shares, the necessary rate of return is the lowest rate of return that investors are willing to accept.
All efforts have been made to ensure the information provided here is accurate. However, no guarantees are made regarding correctness of data. Please verify with scheme information document before making any investment.